Geschichtete Auswahl

Bei der geschichteten Zufallsstichprobe (auch: stratifizierte Zufallsstichprobe) in der Statistik wird die entsprechende Grundgesamtheit in mehrere kleinere Gruppierungen, welche als Schichten bezeichnet werden, unterteilt. Danach zieht man separat aus jeder Gruppierung eine einfache Zufallsstichprobe. Diese Stichproben werden dann beim Schluss auf die Grundgesamtheit entsprechend den Umfängen der einzelnen Schichten, die bekannt sein müssen, gewichtet. Durch Schichtung erhält man bei günstiger Auswahl genauere Ergebnisse, mindestens aber genauso gute Ergebnisse wie bei der einfachen Zufallsstichprobe.

Grundgesamtheitsparameter

• Mittelwert: 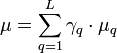$\mu= \sum_{q=1}^L \gamma_q \cdot \mu_q$ mit q = 1...L Schichten; der Auswahlwahrscheinlichkeit 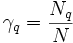$\gamma_q = \frac{N_q}{N}$ und dem Schichtumfang N_q
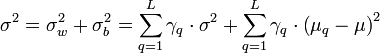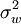• Varianz $\sigma^2 = \sigma^2_w + \sigma^2_b = \sum_{q=1}^L \gamma_q \cdot \sigma^2 + \sum_{q=1}^L \gamma_q \cdot \left( \mu_q - \mu \right)^2$ mit $\sigma^2_w$ Varianz innerhalb der Schichten und 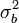$\sigma^2_b$ Varianz zwischen den Schichten

• Anteilswert $\theta= \sum_{q=1}^L \gamma_q \cdot \theta_q$

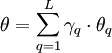
Schätzer für die Grundgesamtheitsparameter

• Schätzer für den Mittelwert: $\hat \mu_{StrRS}= \sum_{q=1}^L \gamma_q \cdot \hat \mu_q$

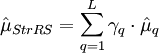
StrRS: Stratified Random Sample: Geschichtete Zufallsauswahl

• Schätzer für die Varianz:

• Schätzer für den Anteilswert

Schichtungsarten

Es gibt verschiedene Arten der Schichtung:

• Gleichaufteilung (Gleiche Auswahl): n₁ = n₂ = ...n_l bei n_q Schichten q = 1,...,L
• Proportionale Auswahl: Werden die Stichproben in ihrer Größe den jeweiligen Anteilen der Schichten in der Grundgesamtheit entsprechend gezogen, bezeichnet man die Auswahl als "proportional geschichtet".
• Disproportionale Auswahl: Weichen die Fallzahlen der jeweiligen Stichproben dagegen von den Anteilen der Grundgesamtheit ab, spricht man von "disproportional geschichteten Auswahlen".
  • Optimale Auswahl: Die Optimale Auswahl berücksichtigt die einzelnen Streuungen in den Schichten. Aus einer Schicht mit größerer Varianz werden mehr Elemente ausgewählt.
  • Kostenoptimale Auswahl

Beispiel: Wenn zum Beispiel bekannt ist, dass größere Werte einer stetigen Schichtungsvariable sehr selten vorkommen (z.B. beim Einkommen), kann man sie als Schicht mit einer größeren Wahrscheinlichkeit auswählen und so genauere Aussagen machen. Bei der Messung der Einkommensverteilung wird Schichtung fast immer eingesetzt, da es nur sehr wenige Einkommensbezieher mit sehr hohem Einkommen gibt und über diese statistische Aussagen von Interesse sind.

Stratifikationsproblematik

Stratifikation ist die Einteilung der Grundgesamtheit in Schichten. Dabei entstehen zwei Teilprobleme:

1. Die Festlegung der Anzahl der Schichten.
2. Die Festlegung der Schichtabgrenzung.

Ziel ist es, die beiden Teilprobleme so zu lösen, dass die Schätzungen genauer werden. Dazu bedarf es allerdings meist Vorinformationen über die Grundgesamtheit (etwa durch die Amtliche Statistik oder vorhergehende Untersuchungen).

Eine Lösung o.g. Problematik stellt etwa das Stratifikationsmodell nach Dalenius inklusive entsprechender Näherungslösungen wie die cum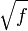$\sqrt{f}$-Regel oder die equal aggregate σ-Regel dar.

Weblinks

http://www.lrz-muenchen.de/~wlm/ilm_a19.htm