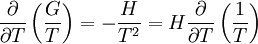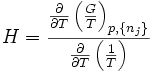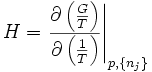- Gibbs-Helmholtzsche Gleichung
-
Die Gibbs-Helmholtz-Gleichung (auch Gibbs-Helmholtzsche Gleichung)
besagt unter anderem:G : freie Enthalpie
H : Enthalpie
p : Druck
nj : Stoffmenge der Komponente j
Die geschweiften Klammern um die Stoffkomponenten nj sollen andeuten, dass damit die Aufzählung aller unterschiedlichen Komponten j im System gemeint ist. Dies gilt natürlich nur für ein offenes System, bei dem ein Stoffaustausch möglich ist. Bei geschlossenen Systemen entfällt diese Abhängigkeit.
Inhaltsverzeichnis
Herleitung
Die allgemeine Beziehung zwischen der Gibbs-Enthalpie G(T,p,{nj}) und der Inneren Energie U(S,V,{nj}) eines Systems lässt sich über eine entsprechende Legendre-Transformation herstellen:
oder in differentieller Form ausgedrückt:
μj ist das chemische Potential der jeweiligen Komponente j.
Die Legendre-Transformation zwischen der Enthalpie H und der Gibbs-Enthalpie G lautet:
Wird nun der Ausdruck für die Entropie S aus der differentiellen Form hierhin substituiert folgt:
Nach Anwendung der Quotientenregel der Differentialrechnung:
Dies entspricht der Eingangs genannten Gleichung.
Weitere Schreibweisen
Nach weiteren Zusammenfassungen lässt sich noch eine andere Form der Gleichung angeben:
also:
Mit Hilfe der Kettenregel der Differentialrechnung kann man nun außerdem zeigen, dass gilt:
Auch die Beziehung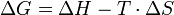 , eigentlich nur eine Legendre-Transformation, die die Beziehung zwischen der Enthalpie H und der Gibbs-Energie G beschreibt, wird in einigen Literaturstellen als Gibbs-Helmholtz-Gleichung bezeichnet (s. Gibbs-Energie). Dies ist wohl dem Umstand zu verdanken, dass man ausgehend von der Legendre-Transformation ausschließlich mathematische Operationen der Differentialrechnung durchzuführen hat, um auf die Gleichung zu kommen, die gemeinhin als Gibbs-Helmholtz-Gleichung bezeichnet wird.
, eigentlich nur eine Legendre-Transformation, die die Beziehung zwischen der Enthalpie H und der Gibbs-Energie G beschreibt, wird in einigen Literaturstellen als Gibbs-Helmholtz-Gleichung bezeichnet (s. Gibbs-Energie). Dies ist wohl dem Umstand zu verdanken, dass man ausgehend von der Legendre-Transformation ausschließlich mathematische Operationen der Differentialrechnung durchzuführen hat, um auf die Gleichung zu kommen, die gemeinhin als Gibbs-Helmholtz-Gleichung bezeichnet wird.In der vorliegenden Vereinfachung wurde ΔS eingeführt, welches die Änderung der Entropie des zu betrachtenden Systems angibt. Dabei ist die Entropie ein Maß für die Unordnung. Somit beinhaltet die Gibbs-Helmholtz-Gleichung auch die Aussage des 2. Hauptsatzes der Wärmelehre, wonach die Natur möglichst energiearme Zustände anstrebt (ungeordnete Zustände).
Vorgänge mit positivem ΔG werden als endergonisch, solche, bei denen die Änderung der Gibbs-Energie negativ ist, als exergonisch bezeichnet. Exergonische Prozesse laufen freiwillig ab, während endergonische Prozesse nur unter Zufuhr von Gibbs-Energie ablaufen.
Eine Sonderstellung nimmt ΔG = 0 ein: Das System befindet sich im Gleichgewicht!
Siehe auch
- Exergon/Endergon
- Gibbs-Energie (Freie Enthalpie)
Literatur
Wikimedia Foundation.

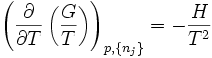
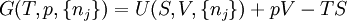
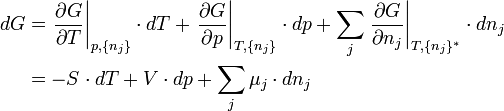
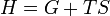
![H = - \left[ -G + T(-S) \right] = -\left[ -G + T \left.\frac{\partial G}{\partial T}\right|_{p,\{n_j\}} \right]](/pictures/dewiki/56/8656fd6578993dc420ab502a8d6b223c.png)
![H =
-\left[\frac{\frac{\partial G}{\partial T}\cdot T - G \cdot \frac{\partial T}{\partial T}}{T^2}
\right] \cdot T^2 = - \frac{\partial}{\partial T}\left(\frac{G}{T}\right)_{p,\{n_j\}} \cdot T^2](/pictures/dewiki/57/98a4dec24146b23078fd9b535e08d087.png)