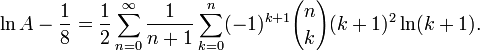- Glaishersche Konstante
-
Die Konstante von Glaisher-Kinkelin, oft auch nur glaishersche Konstante, ist eine mathematische Konstante, die in einigen Summen und Integralen auftritt, vor allem in Zusammenhang mit der Gammafunktion und der riemannschen Zetafunktion. Sie ist nach James Whitbread Lee Glaisher (1848–1928) und Hermann Kinkelin (1832–1913) benannt.
Inhaltsverzeichnis
Näherungswert
Die Konstante von Glaisher-Kinkelin wird üblicherweise mit A bezeichnet. Ein Näherungswert ist
- A = 1,282427129100622636875342568869791727767688927325001192063740021740406308858826
- 46112973649195820237439420646120399000748933157791362775280404159072573861727522... [1]
Die einzelnen Nachkommastellen bilden die Folge A074962 in OEIS.
Definitionen
Eine mögliche Definition von A ist
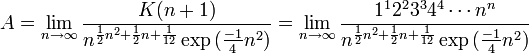 , [2]
, [2]
wobei K(n + 1) die K-Funktion bezeichnet.
Eine andere Definition ist
die den ersten Zusammenhang zur Ableitung der riemannschen Zetafunktion ζ darstellt.
Eine weitere Definition unter Verwendung der Kreiszahl π lautet:
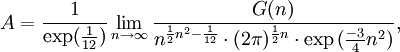 ,
,
wobei G(n) die barnessche G-Funktion bezeichnet.
Eine andere Möglichkeit mit der Gammafunktion Γ ist:
Eine Reihendarstellung lautet (nach Guillera und Sondow, 2005)
Weblinks
- Eric W. Weisstein: Glaisher-Kinkelin Constant auf MathWorld (englisch)
Einzelnachweise
- ↑ Die ersten 20.000 Nachkommastellen unter http://mpmath.googlecode.com/svn/data/glaisher.txt
- ↑ Julian Havil: Gamma: Eulers Konstante, Primzahlstrände und die riemannsche Vermutung. Springer-Verlag, Berlin 2007, ISBN 978-3-540-48495-0, S. 103
- A = 1,282427129100622636875342568869791727767688927325001192063740021740406308858826
Wikimedia Foundation.

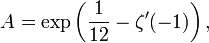
![A = 2^{7/36}\pi^{-1/6}\exp \left(\frac 13 +\frac 23 \int\limits_0^{1/2} \ln\left[\Gamma(x+1)\right]\mathrm dx\right).](/pictures/dewiki/51/3210340c787c023853869dda7732976c.png)