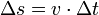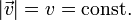- Gradlinige Bewegung
-
Eine gleichförmige Bewegung (gleichförmige Translation) ist eine Bewegung, die durch konstante Geschwindigkeit gekennzeichnet ist.
Oft wird der Begriff durch das Wort "geradlinig" ergänzt. Dies ist aber nicht nötig, da jede gleichförmige Bewegung geradlinig ist.
Die gleichförmige Bewegung ist ein Spezialfall der gleichmäßig beschleunigten Bewegung mit der Beschleunigung
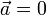 .
.Inhaltsverzeichnis
Definition und Gesetze
Eine Bewegung heißt gleichförmig, wenn der Geschwindigkeitsvektor
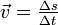 konstant ist. Dies bedeutet, dass sich weder der Betrag der Geschwindigkeit, noch die Bewegungsrichtung ändert. Dabei steht v für die Geschwindigkeit und Δs für die Länge der Stecke, die während der Zeitdifferenz Δt zurückgelegt wird
konstant ist. Dies bedeutet, dass sich weder der Betrag der Geschwindigkeit, noch die Bewegungsrichtung ändert. Dabei steht v für die Geschwindigkeit und Δs für die Länge der Stecke, die während der Zeitdifferenz Δt zurückgelegt wirdΔt wird verwendet, weil man hier keine absolute Zeit einsetzen darf (z.B. 30. April 14:00 Uhr), sondern eben nur Zeitdifferenzen, z.B. 10 min.
Die während der Zeitdifferenz Δt zurückgelegte Strecke Δs lässt sich in diesem Fall berechnen durch
Für die Gesamtstrecke s(t) zur Zeit t gilt dann
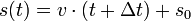 .
.
Dabei steht t für die Zeit, Δt für die Zeitdifferenz vom Start der Beobachtung bis zum Ende,
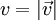 für den Betrag der Geschwindigkeit und s0 für die Anfangsstrecke.
für den Betrag der Geschwindigkeit und s0 für die Anfangsstrecke.Vektorbasierte Definition
Etwas allgemeiner sind die folgenden, vektoriell formulierten Gesetze:
- Beschleunigungs-Zeit-Gesetz:
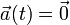
- Geschwindigkeits-Zeit-Gesetz:
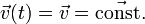 (definitionsgemäß)
(definitionsgemäß)
- Weg-Zeit-Gesetz:
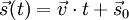
Dabei bezeichnen:
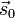 : Ortsvektor zur Zeit t = 0
: Ortsvektor zur Zeit t = 0 : Geschwindigkeit
: Geschwindigkeit : Beschleunigung
: Beschleunigung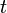 : Zeit
: Zeit
Nach dem Trägheitssatz bewegt sich jeder Körper, auf den keine resultierende Kraft (Gesamtsumme Kräfte gleich Null) wirkt, gleichförmig. (Die Möglichkeit, dass der Körper in Ruhe verharrt, kann als gleichförmige Bewegung mit der Geschwindigkeit 0 aufgefasst werden.)
Allgemeinere Verwendung des Begriffs
Gelegentlich wird unter gleichförmiger Bewegung auch die Bewegung mit konstantem Geschwindigkeitsbetrag verstanden, also
Die Geschwindigkeit der Bewegung kann unterschiedliche Richtungen haben, aber der Betrag ist konstant. Ein wichtiges Beispiel ist die gleichförmige Kreisbewegung (gleichförmige Rotation). Trotz dieser Bezeichnung handelt es sich um eine beschleunigte Bewegung, da eine zum Kreismittelpunkt gerichtete Zentripetalbeschleunigung auftritt. Eine gleichförmige Kreisbewegung setzt also das Vorhandensein einer Zentripetalkraft voraus.
Siehe auch
- Bahngeschwindigkeit – mit einer Analyse verschiedener Spezialfälle der Bewegungsgeschwindigkeit
Wikimedia Foundation.