Graphzeichnen

Das Graphzeichnen (engl. Graph Drawing) ist ein Themengebiet der Informatik, das sich damit beschäftigt, Algorithmen zu entwickeln, die Graphen auf dem Bildschirm oder auf Papier darstellen können. Graphzeichnen ist dabei in zwei Felder unterteilt: Im statischen Graphzeichnen soll ein Graph dargestellt werden, während im dynamischen Graphzeichnen ganze Sequenzen von Graphen (meist in einer Animation) visualisiert werden sollen.

Ansätze

Im Graphzeichnen gibt es keine universellen Techniken, die einen Graphen zeichnen können. Je nach Anwendungsgebiet sind unterschiedliche Ansätze notwendig, die den jeweilig zu erzielenden Effekt unterstreichen. Die folgenden Erklärungen gelten sowohl für das statische, als auch für das dynamische Graphzeichnen.

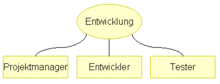
Hierarchisches Zeichnen

Hierbei versucht man aus einem gerichteten Graph eine Hierarchie auszulesen und diese dann angemessen darzustellen. Dazu wird die Knotenmenge in Äquivalenzklassen aufgeteilt, so dass Knoten einer Äquivalenzklasse auf einer Höhe gezeichnet werden. Dadurch entsteht eine Zeichnung, die die im Graph vorherrschende Hierarchie herausstellt.

In der Geschäftsprozessmodellierung werden hierarchische Graphen u. a. für Wertschöpfungskettendiagramme oder Organigramme verwendet.

Ausrichtung am längsten Pfad

Dabei wird zwischen allen Start-Knoten (Knoten ohne Vorgänger) und End-Knoten (Knoten ohne Nachfolger) diejenige Kombination ermittelt, bei der der Pfad zwischen Start- und End-Konten die größte Anzahl dazwischen liegender Knoten aufweist. Dieser längste Pfad wird dann zur Basis für die Ausrichtung aller Knoten und Kanten, wobei die im längsten Pfad liegenden Knoten und Kanten möglichst an einer Gerade ausgerichtet werden die nicht im längsten Pfad liegenden Knoten und Kanten um die Gerade herum angeordnet werden.

In der Geschäftsprozessmodellierung werden am längsten Pfad ausgerichtete Graphen u. a. für EPKs verwendet. Dabei ist die Anwendung von Autolayout-Algorithmen zur Berechnung eines am längsten Pfad ausgerichteten Graphen ein Problem mit erheblichem Entwicklungspotential.

In der Softwaremodellierung kann diese Darstellung in den Notationen BPMN und UML verwendet werden.

Kräftebasiertes Zeichnen

Diesem Ansatz liegt das Modell zugrunde, dass auf alle Knoten Kräfte wirken. Diese Kräfte ergeben sich in diesem Modell durch die Kanten. Anschließend bestimmt man die Gesamtkraft, die auf jeden Knoten wirkt und kann so die Positionen der Knoten in der Zeichnung erhalten. Kanten werden bei diesem Ansatz immer durch gerade Linien repräsentiert^[1]. Darüber hinaus können komplexere mathematische oder pseudo-physikalische Modelle für die Berechnung der Kräfte angewandt werden. So können sich z.B. alle Knoten gegenseitig abstoßen (ähnlich einer elektrostatischen Kraft). Knoten können auch mit unterschiedlicher Dichte in einem flüssigen Medium simuliert werden, so dass einzelne Knoten mehr oder weniger Auftrieb erfahren. Auf diese Weise ergeben sich natürlicher anmutendende und oft intuitiver interpretierbare Zeichnungen des Graphen ^[2].

Skizzenbasiertes Zeichnen

In diesem Fall liegt bereits eine Skizze eines Graphen vor. Daraus wird dann ein Bild für den Graph erzeugt. Diese Methode findet zum Beispiel beim Vereinfachen von Landkarten Anwendung: Bestimmte Orte werden aus der Landkarte herausgefiltert und anschließend werden Straßen zwischen den ausgewählten Orten durch Kanten repräsentiert. In einer Zeichnung dieses Graphen werden dann alle Knoten an die Positionen gezeichnet, an denen sie schon in der Landkarte erschienen. Kanten verlaufen dann (meist als gerade Linien) gegenseitig ausgerichtet. Das resultierende Bild kann zum Beispiel als Anfahrtskizze oder für Busfahrpläne benutzt werden.

Arten von Zeichnungen

Je nach gewünschtem Ergebnis teilt man die Art der Zeichnungen in folgende Klassen ein:

Orthogonale Zeichnung

Orthogonale Verbindung von Knoten eines Graphen

Kanten sind in orthogonalen Zeichnungen immer als Linienzüge dargestellt, die an Ecken miteinander verbunden sind. Alle Linienzugsegmente verlaufen dabei innerhalb der Zeichnung vertikal oder horizontal, aber nie diagonal. Beispiele sind u.a. Organigramme^[3][4].

Spline-Zeichnung

Spline-Verbindung von Knoten eines Graphen

Die Kanten werden hierbei durch geschwungene Linien repräsentiert, die keine Knicke aufweisen. Dies kann zum Beispiel durch den Einsatz von Bezierkurven oder B-Splinekurven erreicht werden.

Beispiele hierzu siehe ^[5][6]

Anforderungen an Zeichnungen

Die Darstellung eines Graphen sollte auf einen Betrachter auf keinen Fall verwirrend wirken, sondern sollte die besonderen Eigenschaften des zugrundeliegenden Graphen betonen. Dabei ist die Auswahl des Algorithmus zur Berechnung der Darstellung ausschlaggebend. Dieser Algorithmus soll eine möglichst ästhetische Darstellung des Graphen realisieren. Was als möglichst ästhetische Darstellung angesehen wird ist jedoch einerseits vom persönlichen Empfinden des Betrachters und andererseits vom beabsichtigten Zweck der Darstellung abhängig. Es gibt dennoch messbare Kriterien, nach denen die Eignung der Darstellung für einen beabsichtigten Zweck beurteilt werden kann, wie

• den minimalen Abstand und die minimale Größe der Knoten, beeinflusst durch die Auflösung des darstellenden Gerätes,
• den maximalen Abstand und die maximale Größe der Knoten, beeinflusst durch die Anzeigefläche des darstellenden Gerätes,
• die Varianz der Kantenlängen und Knotengrößen (gleiche Größe, am goldenen Schnitt abgestuft, beliebige Größe),
• die Anzahl der Kantenkreuzungen,
• die Anzahl der Kantenknicke (bei orthogonalen Kanten) oder Kantenstützpunkte (bei Spline-Kanten),
• den Abstand benachbarter Knoten zueinander (als Maß für die freie Fläche zwischen zwei Knoten) oder
• Symmetrien wie horizontale, vertikale, diagonale, radiale Ausrichtung oder gleichartige Strukturen in Teilgraphen.

Eine besondere Eigenschaft von Graphen sind zum Beispiel das Vorhandensein von Quellen (Knoten ohne eingehende Kanten) oder Senken (Knoten ohne ausgehende Kanten). Diese Eigenschaft wird von einem hierarchischen Layoutalgorithmus oder einem Layoutalgorithmus zur Ausrichtung am längsten Pfad besonders hervorgehoben.

Im dynamischen Graphzeichnen ist zusätzlich wichtig, dass aufeinanderfolgende Graphen nicht zu unterschiedlich gezeichnet werden. Knoten, die beispielsweise von einem Graph zum nächsten beibehalten werden, sollten möglichst ihre Position behalten. An dieser Stelle geht man davon aus, dass ein Graph eine sogenannte Mental Map besitzt, die von einem Betrachter meist unterbewusst wahrgenommen wird. Das Ziel ist es nun, die Mental Map über die gesamte Sequenz zu erhalten.

Bemerkungen

Die Graphdrawing-Community ist derzeit aktiver denn je. So waren bei der Graphdrawing-Conference im Oktober 2004 weitaus mehr eingereichte Abhandlungen vertreten als in den Jahren zuvor. Derzeit liegt das Hauptaugenmerk der Forschung auf der Verbesserung von langsamen Algorithmen. Da viele Problemstellungen im Zusammenhang mit Graphzeichnen NP-vollständig sind, ist das Berechnen eines optimalen Layouts (optimal im Sinne des Zeichners) sehr langwierig. Daher versucht man, neue Algorithmen zu entwickeln, die möglichst schnell arbeiten und deren Ergebnisse trotzdem nahe an der optimalen Lösung liegen.

Anwendungen

Graphzeichnen findet Anwendung beim automatischen Anordnen von auf Graphen basierenden Diagrammtypen unterschiedlichster Art, etwa bei der Geschäftsprozessmodellierung oder der Softwaremodellierung. Die Autolayout-Algorithmen zum Erstellen der Zeichnungen finden sich auch in spezialisierten kommerziellen Software-Bibliotheken^[7].

Software Anwendungen wie der Diagrammeditor yEd bieten umfangreiche Unterstützung für hierarchisches, kräfte- und skizzenbasiertes Zeichnen und ermöglichen sowohl statisches als auch dynamisches Graphzeichnen.

Einzelnachweise

1. ↑ Force-directed layout (in Englisch)
2. ↑ Found in Space — 3-dimensionale Anzeige für agile semantische Netze
3. ↑ Organigramm
4. ↑ aiSee.com Graphen-Datenbank (in Englisch)
5. ↑ Unix-Evolution
6. ↑ aiSee.com Graphen-Datenbank, Splines Examples (in Englisch)
7. ↑ Graphzeichnen Software-Bibliotheken

Weblinks

• Das Graphzeichnen-Portal
• Die Graphzeichnen-Konferenz 2004 - New York, USA
• Die Graphzeichnen-Konferenz 2005 - Limerick, Irland
• Die Graphzeichnen-Konferenz 2006 - Karlsruhe, Deutschland
• Das Graphzeichnen-Projekt an der katholischen Universität Eichstätt (Bayern)
• Links zum Thema Graphzeichnen im Open Directory Project