Graycode

Eigenschaften
Hamming-Distanz	1
Stetig	ja

Der Gray-Code (nach dem Physiker Frank Gray) ist ein stetiger Code, bei dem sich benachbarte Codewörter nur in einer einzigen dualen Ziffer unterscheiden. Die Hamming-Distanz aller benachbarter Codewörter ist somit 1. Dadurch verringert sich der maximal mögliche Ablesefehler bei der Quantisierung aus einem Analogsignal auf einen Code. Er dient als Kodierungsverfahren zur robusten Übertragung digitaler Größen über analoge Signalwege. Meistens ist er als Binärcode ausgeführt, kann aber auch für mehrstufige Übertragungswege benutzt werden.

Generierung aus Binärcode

Die folgenden Punkte zeigen, wie man Schritt für Schritt aus einer binär codierten Dezimalzahl (Binärcode) eine Gray-codierte Binärzahl erhält:

• X1: Dualzahl im Binärcode
• X2: Links-Shift der Dualzahl um 1 Bit
• X3: Modulo-2-Addition (XOR-Verknüpfung) von X1 und X2
• X4: Rechts-Shift der Dualzahl um 1 Bit; dies ist die gewünschte Zahl im Graycode.

Das gleiche als Programmcode:

• Binärcode X1 --> Graycode: X4 = ((X1*2) XOR X1) / 2

Beispiel:

• Man möchte die Zahl X1 = 12₁₀ = 1100₂ (Binärcode) in den Graycode konvertieren:
• Der Links-Shift um 1 Bit liefert X2 = 11000₂;
• mit der Modulo-2-Addition(Binäre Addition ohne Übertrag) berechnet man X3 = X1 ⊕ X2 = 1100₂ ⊕ 11000₂ = 10100₂ und
• nach dem Rechts-Shift erhält man nun die Zahl im Gray-Code: X4 = 1010₂.

Ein einfacherer Weg wäre folgender:

• X1: Dualzahl im Binärcode
• X2: Rechts-Shift der Dualzahl um 1 Bit
• X3: Modulo-2-Addition (XOR-Verknüpfung) von X1 und X2; dies ist die gewünschte Zahl im Graycode.

Das gleiche als Programmcode:

• Binärcode X1 --> Graycode: X3 = (X1 XOR (X1/2))

Generierung als Gray-Zähler

"Man kann auch direkt einen Gray-Code-Zähler in Hardware (z.B. in HDL) programmieren. Hierzu ist es hilfreich ein Hilfsregister hinzu zu nehmen, das mit jedem Taktzyklus toggelt.

Q_h [n+1] = !Q_h [n]

Damit wird die Kombinatorik recht übersichtlich:

Q₀ [n+1] = ! ( Q₀ [n] ^ Q_h [n] )

Q₁ [n+1] = Q₁ [n] ^ ( Q₀ [n] & Q_h[n] )

Q₂ [n+1] = Q₁ [n] ^ ( Q₁ [n] & !Q₀ [n] & Q_h [n] )

Q₃ [n+1] = Q₃ [n] ^ (Q₂ [n] & !Q₁ [n] & !Q₀ [n] & Q_h [n] )

...

Q_k-1 [n+1] = Q_k-1 [n] ^ ( Q_k-2 [n] & !Q_k-3 [n] & ... & !Q₁ [n] & !Q₀ [n] & Q_h [n] )

Q_k [n+1] = Q_k [n] ^ ( !Q_k-2 [n] & !Q_k-3 [n] & ... & !Q₁ [n] & !Q₀ [n] & Q_h [n] )

^ := XOR / Exklusiv Oder / Antivalenz
! := Inverter / Not / Negation
& := Und / And /Konjunktion"

Bedeutung

Ausgangspunkt für diesen Code ist das folgende Problem: Auf mehreren Adern einer elektrischen Datenleitung sollen Daten parallel übertragen werden, die sich stetig (also nicht sprunghaft) ändern, z. B. Signale eines Temperatursensors in einem Ofen. Theoretisch ändern sich die Bits bei einem neuen Messwert auf jeder betroffenen Leitung exakt gleichzeitig, und zwar sowohl am Eingang der Leitung als auch am Ausgang. Tatsächlich aber ändern sich die Bits auf der Leitung nicht gleichzeitig. Das kann verschiedene Ursachen haben: Bauteilestreuung, Laufzeiten, Asymmetrien usw. Dadurch kommt es zu ungewollten Zwischenzuständen:

2-Bit-Gray-Code: 00 01 11 10 3-Bit-Gray-Code: 000 001 011 010 110 111 101 100 4-Bit-Gray-Code: 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 5-Bit-Gray-Code: 00000 00001 00011 00010 00110 00111 00101 00100 01100 01101 01111 01110 01010 01011 01001 01000 11000 11001 11011 11010 11110 11111 11101 11100 10100 10101 10111 10110 10010 10011 10001 10000

6-Bit-Gray-Code: 000000 000001 000011 000010 000110 000111 000101 000100 001100 001101 001111 001110 001010 001011 001001 001000 011000 011001 011011 011010 011110 011111 011101 011100 010100 010101 010111 010110 010010 010011 010001 010000 110000 110001 110011 110010 110110 110111 110101 110100 111100 111101 111111 111110 111010 111011 111001 111000 101000 101001 101011 101010 101110 101111 101101 101100 100100 100101 100111 100110 100010 100011 100001 100000

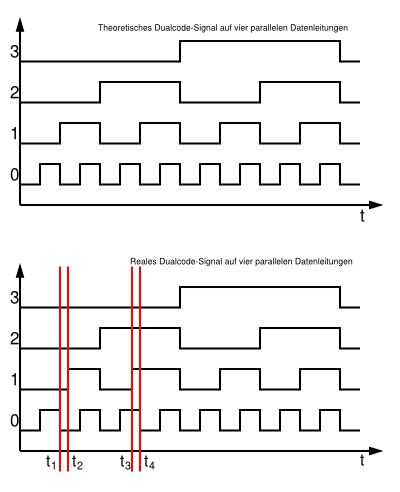
Problem bei Dualcode-Signalen

Während das theoretische Signal in der Reihenfolge

• {0000}, {0001}, {0010}, {0011}, {0100}, {0101}, {0110}, {0111}, usw.

abgesendet wird, kommen am Ausgang kurzzeitig andere Signalzustände an:

• {0000}, {0001}, {0000}, {0010}, {0011}, {0100}, {0101}, {0111}, {0110}, {0111}, usw.

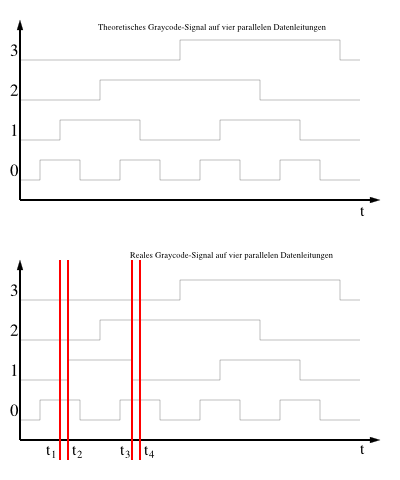
Lösung mit Gray-Code

Um das zu vermeiden, werden mittels Gray-Code Steuersignalzustände in einer Sequenz abgesendet, bei denen sich immer nur ein Bit gleichzeitig ändert:

• Abgesendete Sequenz: {0000}, {0001}, {0011}, {0010}, {0110}, {0111}, {0101}, {0100}, usw.
• Ankommende Sequenz: {0000}, {0001}, {0011}, {0010}, {0110}, {0111}, {0101}, {0100}, usw.

Hier kommt also am Ausgang die gleiche Sequenz wie am Eingang an.

Karnaugh-Veitch-Diagramm

Im Karnaugh-Veitch-Diagramm erkennt man den Graycode – es sind mehrere Sequenzen möglich – daran, dass Übergänge nur zwischen benachbarten Feldern vorkommen.

Reihenfolge bei Dualcode   ¬X0 X0 X0 ¬X0   ¬X2 0 1 3 2 ¬X3 X2 4 5 7 6 ¬X3 X2 12 13 15 14 X3 ¬X2 8 9 11 10 X3   ¬X1 ¬X1 X1 X1

Reihenfolge bei Graycode   ¬X0 X0 X0 ¬X0   ¬X2 0 1 2 3 ¬X3 X2 7 6 5 4 ¬X3 X2 8 9 10 11 X3 ¬X2 15 14 13 12 X3   ¬X1 ¬X1 X1 X1

Der Code eignet sich auch für zyklische Anwendungen wie der unten abgebildeten Scheibe, da sich auch beim Übergang von der höchsten Zahl auf die Null nur eine Stelle ändert.

Die Wertigkeit einer 1 an der Position n im Gray-Code Zahlensystem ist 2ⁿ − 1 (wobei n ab 1 zählt, also ... 31, 15, 7, 3, 1). Die einzelnen Einsen werden, im Gegensatz zum normalen Binärsystem, nicht addiert, sondern von rechts beginnend subtrahiert. Beispiel: 111_Gray = 7 - (3 - 1) = 5 oder 1111_Gray = 15- (7 - (3 - 1)) = 10. Stellen, die 0 sind, werden dabei ausgelassen, Beispiel: 101_Gray = 7 - 1 = 6.

Bei der Generierung von Gray-Code wird symmetrisch vorgegangen.

Da sich benachbarte Werte nur in einer Ziffer unterscheiden, ist der Gray-Code geeignet, um Fehler in seriellen Prozessen aufzudecken.

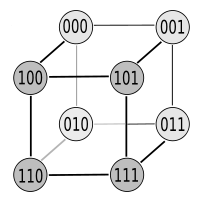
Hyperwürfel

Bild 1: Hyperwürfel

Bild 2: Hyperwürfel mit Koordinatensystem

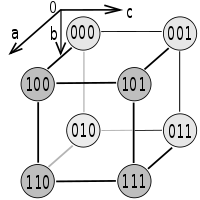
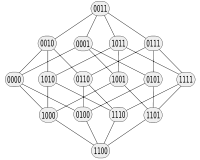
Bild 1 zeigt den Hyperwürfel für 3 Variablen und Bild 2 den gleichen Würfel mit dazugehörigem Koordinatensystem. Die Knoten (Eckpunkt oder Kreise) am Hyper-Einheitswürfel entsprechen jeweils einer Zeile im Gray-Code. Die Übergänge (Nachbarschaft der Zeilen) sind durch die Kanten des Würfels symbolisiert. Beim Wandern auf der Kante entsteht ein Gray-Code.

geschlossener 3-Bit-Gray-Code
a)	b)	c)	d)	e)	f)
000	000	000	000	000	000
001	100	010	010	001	100
101	101	110	011	011	110
100	001	100	001	010	010
110	011	101	101	110	011
111	111	111	111	111	111
011	110	011	110	101	101
010	010	001	100	100	001

Auf jeder Kante ändert sich genau 1 Bit. Der Gray-Code hat so viel Nachbarschaften, wie der Würfel Kanten hat. Aus dem Hyperwürfel in Bild 1 können die möglichen Pfade auf 6 verschiedenen Wegen durchschritten werden. Somit ergeben sich 6 Möglichkeiten, um einen 3-Bit-Gray-Code zu erzeugen, der die Bedingungen des Gray-Codes erfüllt (Tabelle und Bild 3). Abgesehen davon ist der Gray-Code zyklisch und der Startpunkt könnte deshalb auch an einer anderen Zeile sein. Wegen seiner einfachen rekursiven Generierungsvorschrift wird meist der binäre reflektierte Gray-Code (binary-reflected Gray code) angegeben (Spalte "e" – vorletzte Spalte in der Tabelle). Es gibt für eine bestimmte Bitlänge eine ganze Klasse von Graycodes. Es gibt für einen n-Bit-Gray-Code exakt so viel Varianten, wie es Hamiltonkreise auf einem n-dimensionalen Hyperwürfel gibt.

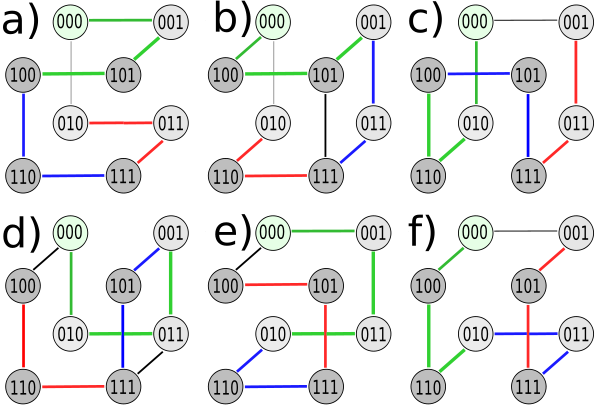Bild 3: Die 6 Pfade zu dem Gray-Code in der Tabelle. Es handelt sich um einen Hamiltonkreis. Startpunkt: 000 (grüner Kreis jeweils links oben), Fortsetzung: grüne->blaue->rote->schwarze Linie, Endpunkt: am Startpunkt

geschlossener 3-Bit-Gray-Code
a)	b)	c)	d)	e)	f)
000	000	010	010	000	100
001	100	110	011	001	110
101	101	100	001	011	010
100	001	101	101	010	011
110	011	111	111	110	111
111	111	011	110	111	101
011	110	001	100	101	001
010	010	000	000	100	000

Da der hier dargestellt Gray-Code zyklisch ist, wurde in dieser Tabelle der Code in den Spalten c), d) und f) um eine Stelle nach oben verschoben (im Vergleich zur Tabelle weiter oben), so dass jeweils die drei Nullen in der letzten Tabellenzeile stehen. So ist erkennbar, dass es sich bei dem Gray-Code in Spalte a) nur um eine spiegelbildliche Umkehrung der Spalte c) handelt. Genauso ist Spalte b) die Umkehrung von Spalte d), während Spalte e) die Umkehrung von Spalte f) ist. Es gibt drei ungerichtete Hamiltonkreise am dreidimensionalen Hyperwürfel, die hier lediglich in unterschiedlicher Richtung (gerichteter Hamiltonkreis) dargestellt wurden.
Zur besseren Veranschaulichung sind hier nochmals die Codetafeln für die 6 Varianten des 3-Bit-Graycodes dargestellt. Wobei die Variante e den binäre reflektierte Gray-Code darstellt, der meist gemeint ist, wenn vom Gray-Code die Rede ist. Die 6 Versionen kan man auch durch Permutation der 3 Spalten der Codetafel erzeugen. Daraus ergibt sich, dass es bei n Bit n! Versionen gibt. Also für 3 Bit 3!= 6 Versionen des 3-Bit-Graycodes..

3 Bit: a

3 Bit: b

3 Bit: c

3 Bit: d

3 Bit: e

3 Bit: f

Bild 4

... usw. ...

Den 4-Bit-Gray-Code kann man aus dem Hyperwürfel in Bild 4 ablesen. Für 4 Bit gibt es 4! = 24 verschiedene Gray-Codes.

Anwendungen

Schemazeichnung einer Scheibe mit Gray-Codierung. Die gelben Punkte stellen Lichtsensoren dar.

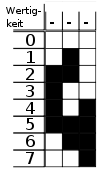
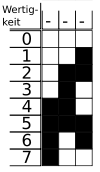
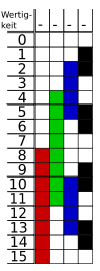
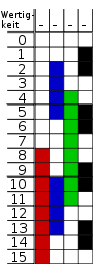
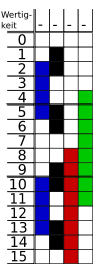
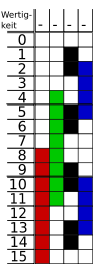
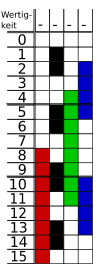
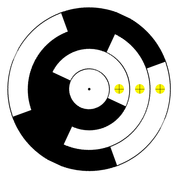
Eine Anwendungsmöglichkeit ist die Bestimmung der absoluten Position einer Scheibe oder Leiste, die mit schwarzen und weißen Balken markiert ist, die mit Lichtschranken oder anderen Sensoren abgetastet werden. Diese Position wird dann zur Winkel- oder Drehgeschwindigkeitsmessung verwendet.

Eine weitere Anwendung ist die Streifenprojektion. Dort wird eine Folge von Mustern aus parallelen Streifen auf ein Objekt projiziert. Die Nummer der Streifen ist Gray-kodiert und kann von einer beobachtenden Kamera für jeden Bildpunkt berechnet werden.

Eine andere Anwendung ist das asynchrone Einlesen von Daten. Beispielsweise wird der Gray-Code genutzt, um in Korrelatoren die Zählerstände fehlerfrei einzulesen. Selbst im ungünstigsten Fall, wenn während eines kippenden Bits eingelesen wird, ist das Ergebnis immer korrekt, da ein kippendes Bit nicht definiert ist und es zudem nur einen Unterschied von ±1 ausmacht. Diese Art des Einlesens erfordert keine Synchronisation und nur sehr wenig CPU-Zeit.

Weitere Anwendungsmöglichkeiten sind Windrichtungsmesser oder Wasserniveaumesser, Abbildung des Fahrkorbstands bei Aufzügen.

Der reflektierte Gray-Code hat eine enge Beziehung zur Lösung des Problems der Türme von Hanoi.

Beispiel

Die Dezimalzahl 4₁₀ = 100₂ entspricht dem Gray-Code 6₁₀ = 110₂. Die Dekodierung in die Dezimaldarstellung folgt dann der Regel 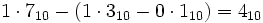$1\cdot 7_{10} - (1\cdot 3_{10} - 0\cdot 1_{10}) = 4_{10}$. Wenn mehrere Einsen in einer Gray-Code-Zahl vorkommen, werden diese voneinander subtrahiert: Der Gray-Code 7₁₀ = 111₂ wird wie folgt dekodiert: $1\cdot 7_{10} - (1\cdot 3_{10} - 1\cdot 1_{10}) = 5_{10}$.

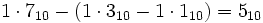Allgemeines Verfahren: Bei einer Umwandlung ist entscheidend, an welcher Position die Einser stehen. Die Position hat Einfluss auf die Rechnung. Wenn wir uns die Zahl 100 anschauen, dann steht die Eins auf Position 3 (von rechts nach links). Den Faktor für die Eins bekommt man, indem man sich überlegt, welche Dezimalzahl maximal in einer 3-Bit Zahl binär gespeichert werden kann. In 3 Bit Binärcode kann maximal die Zahl 7 (111) gespeichert werden. Nehmen wir jetzt eine größere Binärzahl, funktioniert das praktisch analog. Binärzahl: 11010 (1 an Position 5,4 und 2). 5 Bit Binärzahl: max. 31 4 Bit Binärzahl: max. 15 2 Bit Binärzahl: max. 3

Berechnung: 31₁₀ − (15₁₀ − 3₁₀) = 19

Geschichte

Noch bevor die Bezeichnung Gray-Code eingeführt wurde, gab es bereits mathematische Knobelspiele, in denen das Prinzip angewendet wurde. Erst später fand der Code die Beachtung von Ingenieuren. Der Franzose Jean-Maurice-Émile Baudot verwendete Gray-Codes bereits im Jahr 1887 für die elektrische Telegrafie. Er erhielt für seine Arbeit die Auszeichnung der französischen Ehrenlegion.

Namensgebend war allerdings Frank Gray, Forscher in den Bell Laboratories, der den Code erst 1946 für seine Zwecke wiederentdeckte. Unter dem Titel Pulse Code Communications wurde am 17. März 1953 unter der US-Patentnummer 2,632,058 ein Patent für eine Gray-Kodierende Elektronenröhre erteilt.

Siehe auch

• 1-aus-10-Code
• Aiken-Code
• BCD-Code
• Gillham-Code
• Libaw-Craig-Code
• Stibitz-Code

Weblinks

• Java-Beispiel für die Umwandlung einer Dezimalzahl in Gray-Code Darstellung
• Java Applet zur Umwandlung von Gray- in Binärcode und zurück