Hyperwürfel

Projektion eines Tesseraktes (vierdimensionaler Hyperwürfel) in die 2. Dimension

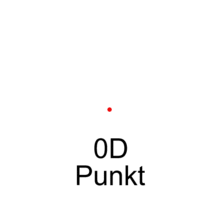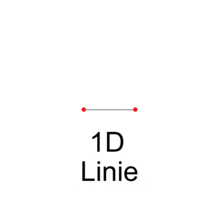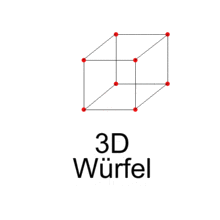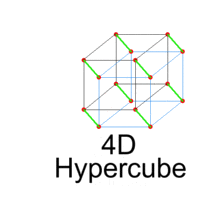
Hyperwürfel sind n-dimensionale Analogien zum Quadrat (n = 2) und zum Würfel (n = 3). Der vierdimensionale Hyperwürfel wird auch als Tesserakt bezeichnet. Es gilt $n \in \N$ (n ist beliebige Natürliche Zahl).

Konstruktion regulärer Würfel

Reguläre Würfel der Kantenlänge a(≠0) lassen sich wie folgt erzeugen:

• Wenn ein Punkt um die Distanz a geradlinig verschoben wird, entsteht eine eindimensionale Strecke, mathematisch ein eindimensionaler Hyperwürfel.
• Wenn diese Strecke senkrecht zu ihrer Dimension um die Distanz a verschoben wird, entsteht ein zweidimensionales Quadrat, eine Fläche, mathematisch ein zweidimensionaler Hyperwürfel.
• Wenn dieses Quadrat senkrecht zu seinen beiden Dimensionen um die Distanz a verschoben wird, entsteht ein dreidimensionaler Würfel, mathematisch einem dreidimensionalen Hyperwürfel entsprechend.
• Allgemein: Wenn also ein n-dimensionaler Würfel senkrecht zu seinen n Dimensionen um die Distanz a verschoben wird, entsteht ein (n+1)-dimensionaler Hyperwürfel.

Grenzelemente

In einem Hyperwürfel der Dimension n befinden sich an jedem Knoten (Ecke) genau n Kanten. Demnach handelt es sich bei einem Hyperwürfel um einen ungerichteten Multigraph (siehe auch: Graphentheorie).

Der n-dimensionale Würfel wird von nulldimensionalen, eindimensionalen, ..., (n-1)-dimensionalen Elementen begrenzt.

Am Beispiel:

Der 3-dimensionale Würfel wird von Knoten (Punkten), Kanten (Strecken) und Flächen begrenzt, also von Elementen der Dimension 0,1 und 2.

Die Anzahl der einzelnen Grenzelemente lässt sich aus folgender Überlegung ableiten: Sei ein Hyperwürfel von der Dimension (n+1). Die k-dimensionalen Grenzelemente dieses Würfels (k_{n + 1}) lassen sich folgendermaßen aus den Grenzelementen eines n-dimensionalen Hyperwürfels erzeugen: Die k-dimensionalen Grenzelemente (k_n) verdoppeln sich und alle k-1 dimensionalen Elemente (k − 1)_n werden zu k-dimensionalen erweitert. Somit ergibt sich in der Summe eine Anzahl von k_{n + 1} = 2k_n + (k − 1)_n.

Beispiel

• Der 2-dimensionale Hyperwürfel wird von 1 Fläche (k_n = 2), 4 Kanten (k_n = 1) und 4 Knoten (k_n = 0) begrenzt.

• Der 3-dimensionale Würfel wird von 2 + 4 = 6 Flächen (k_{n + 1} = 2) begrenzt, von 8 + 4 = 12 Kanten (k_{n + 1} = 1) und 4 + 4 = 8 Knoten (k_{n + 1} = 0).

Anders kann man sich überlegen: Wenn man einen n-dimensionalen Hyperwürfel in ein kartesisches Koordinatensystem um den Ursprung zentriert und nach den Koordinatenachsen ausgerichtet legt, gibt es zu einem k-dimensionalen Grenzelement k Koordinatenachsen, die parallel zu diesem Grenzelement sind. Andererseits gibt es aber zu jeder Auswahl von k Koordinatenachsen nicht nur ein k-dimensionales Grenzelement, sondern 2^n-k, weil man durch jede der n-k zu den Grenzelementen senkrechten Achsen die Anzahl der Grenzelemente verdoppelt (es gibt dieselben Grenzelemente noch einmal parallelverschoben auf der anderen Seite der Achse). Die Anzahl der Grenzelemente ergibt sich also aus dem Produkt der Anzahl der Möglichkeiten, k Achsen aus den n Achsen auszuwählend (Binomialkoeffizient ${n \choose k}$), mit der Anzahl von Grenzelementen für jede Auswahl und lautet somit

${n \choose k} \cdot 2^{n-k}$

Der Weg zum Hyperwürfel

	Anzahl der Grenzelemente
	0-dim.	1-dim.	2-dim.	3-dim.	4-dim.	5-dim.	$\ldots$	(n-1)-dim.
Punkt	1
Strecke	2	1
Quadrat	4	4	1
3-dim. Würfel	8	12	6	1
4-dim. Würfel	16	32	24	8	1
5-dim. Würfel	32	80	80	40	10	1
6-dim. Würfel	64	192	240	160	60	12	1
$\vdots$
n-dim. Würfel	2n	n2n − 1	n(n − 1)2n − 3	$\ldots$	$\ldots$	$\ldots$	$\ldots$	2n

• Alle 0- bis 5-dimensionalen Würfel in der Parallelprojektion
• 

Eigenschaften

Dimension	Kanten	Knoten	Seiten	Grad	Durchmesser	Kanten Zusammenhang	Knoten Zusammenhang
1	1	2	2	1	1	1	1
2	4	4	4	2	2	2	2
3	12	8	6	3	3	3	3
4	32	16	8	4	4	4	4
...	...	...	...	...	...	...	...
n	$2^{(n-1)}\cdot n$	2n	2n	n	n	n	n

Kunstanwendungen

Bildende Kunst

In der Bildenden Kunst beschäftigen sich viele Künstler mit dem Hyperwürfel.

• Tony Robbin – durch Spiegelungen und Verdrehungen von Würfel- Kanten erzeugt Tony Robbin in Zeichnungen und mit Raum-Installationen Situationen, die nur in einer hyperdimensionalen Welt möglich wären.
• Manfred Mohr – veranschaulicht in seinen Kompositionen Interaktionen von Linien, die einer räumlichen Logik von mehr als drei Freiheitsgraden folgen.
• Frank Richter – konkretisiert in Grafiken, Plastiken und Rauminstallationen nach der Vorgabe von mathematischen Regeln Raum-Konstellationen, die über die dritte Dimension hinausgehen.
• Salvador Dalí hat in seinem Bild Kreuzigung (Corpus Hypercubus) 1954 einen gekreuzigten Jesus auf das Netz eines Hyperwürfels gemalt^[1].

Hyperwürfel in der Popkultur

• Der Film Cube 2: Hypercube handelt von einem Hyperwürfel, in dem sich die Charaktere in den drei räumlichen Dimensionen und einer zeitlichen Dimension bewegen und sich beispielsweise selbst in einem anderen Zeitabschnitt begegnen.
• Die Kurzgeschichte And He Built a Crooked House, in der deutschen Version Das 4D-Haus, von Robert A. Heinlein behandelt ein Haus, das aus einem Hyperwürfel besteht.
• Die Metal-Band Tesseract^[2] hat sich nach dem 4D Hyperkubus benannt und verwendet verschiedene Projektionen davon als Bandlogo.

Siehe auch

• 4D
• Euklidischer Raum
• Hyperebene
• Hyperpyramide
• Hyperraum
• Tesserakt

Weblinks

• Der n-dimensionale Hyperwürfel (PDF, ca. 900 kB) – 22. Basler Kolloquium für Mathematiklehrkräfte von Hans Walser, vom 19. November 2003
• Hyperwürfel und Hyperkugeln
• Erweiterte Grenzelemente-Tabelle
• Animierter Hyperwürfel(Java)
• http://www.4d-screen.de/related-space - vier-, fünf-, sechs- und siebendimensionale Würfel (Java)
• Bebilderte Konstruktion eines 4D-Hyperwürfels

Einzelnachweise

1. ↑ Beispiel eines Dalígemäldes
2. ↑ Tesseract