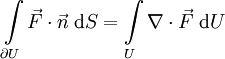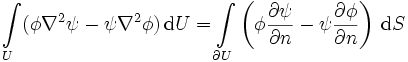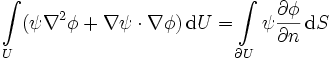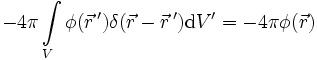Greensche Sätze

In der Mathematik, speziell der Vektoranalysis, sind die beiden greenschen Formeln (manchmal auch greensche Identitäten, greensche Sätze oder Theoreme) spezielle Anwendungen des gaußschen Satzes. Sie sind benannt nach dem Mathematiker George Green. Anwendung finden sie unter anderem in der Elektrostatik bei der Berechnung von Potentialen. Die Formeln sind nicht zu verwechseln mit dem Satz von Green, bei dem es um ebene Integrale geht.

Im folgenden sei 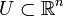$U \subset \mathbb{R}^n$ kompakt mit abschnittweise glattem Rand und φ und ψ seien zwei Funktionen auf U, wobei φ einfach und ψ zweifach stetig differenzierbar sei. $\nabla$ ist der Nabla-Operator.

Erste greensche Identität

$\int\limits_{U} (\phi\nabla ^2\psi + \nabla \phi \cdot \nabla \psi)\, \mathrm{d}U = \int\limits_{\partial U} \phi \frac{\partial\psi}{\partial n} \mathrm{d}S$,

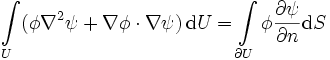wobei 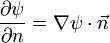$\frac{\partial\psi}{\partial n} = \nabla \psi\cdot\vec{n}$ die Normalenableitung von ψ, also die Normalkomponente des Gradienten von ψ auf dem Flächenelement dS bezeichnet.

Diese Identität lässt sich wie folgt beweisen:

$\int\limits_{\partial U} \phi \frac{\partial\psi}{\partial n} \mathrm{d}S = \int\limits_{\partial U} (\phi\,\nabla\psi)\cdot\vec{n}\,\mathrm{d}S = \int\limits_{U} \nabla\cdot(\phi\,\nabla\psi) \, \mathrm dU = \int\limits_{U} (\nabla\phi\cdot\nabla\psi+\phi\,\nabla^2\psi)\,\mathrm dU$,

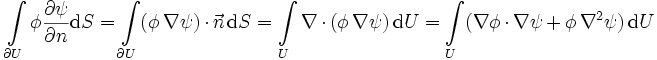wobei im zweiten Schritt der gaußsche Satz in der Form

$\int\limits_{\partial U} \vec F \cdot \vec n\; \mathrm dS = \int\limits_{U} \nabla\cdot \vec F \; \mathrm dU$

benutzt wurde.

Zweite greensche Identität

$\int\limits_{U} (\phi\nabla ^2\psi - \psi\nabla ^2\phi)\, \mathrm{d}U = \int\limits_{\partial U} \left(\phi \frac{\partial\psi}{\partial n} - \psi \frac{\partial\phi}{\partial n}\right) \,\mathrm{d}S$

Die Zweite greensche Identität folgt aus der ersten greenschen Identität:

$\int\limits_{U} (\phi\nabla ^2\psi + \nabla \phi \cdot \nabla \psi)\, \mathrm{d}U = \int\limits_{\partial U} \phi \frac{\partial\psi}{\partial n} \,\mathrm{d}S$,

$\int\limits_{U} (\psi\nabla ^2\phi + \nabla \psi \cdot \nabla \phi)\, \mathrm{d}U = \int\limits_{\partial U} \psi \frac{\partial\phi}{\partial n} \,\mathrm{d}S$

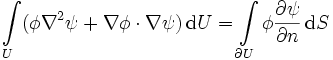Subtrahiert man nun die zweite Gleichung von der ersten Gleichung, so ergibt sich die zweite greensche Identität.

Anwendung in der Elektrostatik

Unter Anwendung der oben gezeigten greenschen Formeln lässt sich das elektrostatische Potential herleiten:

Wir setzen für 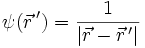$\psi(\vec{r}\,') = \frac{1}{|\vec{r} - \vec{r}\,'|}$, während 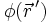$\phi(\vec{r}\,')$ das Potential darstellt. Es gilt dann:

1. $\Delta' \psi(\vec{r}\,') = \Delta'\frac{1}{|\vec{r} - \vec{r}\,'|} = -4\pi \delta(\vec{r} - \vec{r}\,')$,

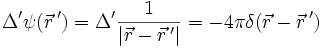   • wobei 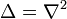$\Delta = \nabla^2$ der Laplace-Operator ist,
   • der Strich anzeigt, dass dieser Operator auf die gestrichene Variable wirkt
   • und δ die Delta-Distribution ist.

   Diese Identität ist also im Sinne von distributionellen Ableitungen zu verstehen.

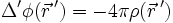2. $\Delta' \phi(\vec{r}\,') = -4\pi \rho(\vec{r}\,')$ mit der Ladungsverteilung ρ am Ort $\vec{r}\,'$.

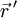Setzen wir beides in die zweite greensche Identität ein, erhalten wir auf der linken Seite:

$\int\limits_{V} (\phi(\vec{r}\,') (-4\pi \delta(\vec{r} - \vec{r}\,')) - \frac{1}{|\vec{r} - \vec{r}\,'|} (-4\pi \rho(\vec{r}\,')))\, \mathrm{d}V' = -4\pi\int\limits_V \phi(\vec{r}\,') \delta(\vec{r} - \vec{r}\,') \, \mathrm{d}V' + 4\pi \int\limits_V \frac{\rho(\vec{r}\,')}{|\vec{r} - \vec{r}\,'|} \, \mathrm{d}V'$.

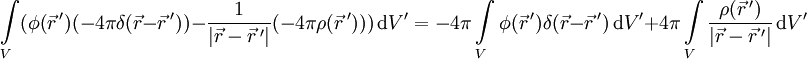Die rechte Seite der Identität ist:

$\int\limits_F \left(\phi(\vec{r}\,') \frac{\partial}{\partial n'}\frac{1}{|\vec{r} - \vec{r}\,'|} - \frac{1}{|\vec{r} - \vec{r}\,'|} \frac{\partial}{\partial n'}\phi(\vec{r}\,') \right) \mathrm{d}F'$.

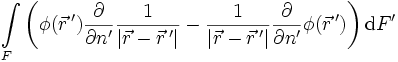Als Identität geschrieben:

$-4\pi \int\limits_V \phi(\vec{r}\,') \delta(\vec{r} - \vec{r}\,') \, \mathrm{d}V' + 4\pi \int\limits_V \frac{\rho(\vec{r}\,')}{|\vec{r} - \vec{r}\,'|} \, \mathrm{d}V' = \int\limits_F \left(\phi(\vec{r}\,') \frac{\partial}{\partial n'}\frac{1}{|\vec{r} - \vec{r}\,'|} - \frac{1}{|\vec{r} - \vec{r}\,'|} \frac{\partial}{\partial n'}\phi(\vec{r}\,') \right) \mathrm{d}F'$.

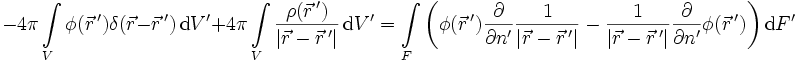Innerhalb des Volumens gilt an der Stelle 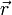$\vec{r}$ wegen der δ-Funktion

$-4\pi \int\limits_V \phi(\vec{r}\,') \delta(\vec{r} - \vec{r}\,') \mathrm{d}V' = -4\pi \phi(\vec{r})$

Damit können wir schliesslich obige Identität nach dem Potential auflösen und erhalten:

$\phi(\vec{r}) = \int\limits_V \frac{\rho(\vec{r}\,')}{|\vec{r} - \vec{r}\,'|} \, \mathrm{d}V' - \frac{1}{4\pi} \int\limits_F \left(\phi(\vec{r}\,') \frac{\partial}{\partial n'}\frac{1}{|\vec{r} - \vec{r}\,'|} - \frac{1}{|\vec{r} - \vec{r}\,'|} \frac{\partial}{\partial n'}\phi(\vec{r}\,') \right) \mathrm{d}F'$.

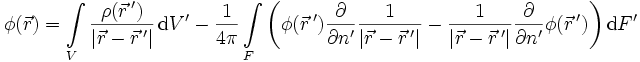Literatur

• John David Jackson: Klassische Elektrodynamik. Walter de Gruyter, Berlin 2006, ISBN 3-11-018970-4
• Walter Greiner: Theoretische Physik Band 3 – Klassische Elektrodynamik. Verlag Harri Deutsch, Frankfurt am Main, Thun ISBN 3-8171-1184-3
• Otto Forster: Analysis 3. Integralrechnung im Rⁿ mit Anwendungen. 3. Aufl. Vieweg-Verlag, 1996. ISBN 3-528-27252-X