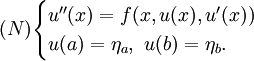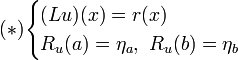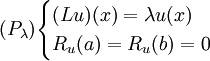Randwertaufgabe

Randwertprobleme (kurz: RWP) auch Randwertaufgabe (kurz: RWA) oder englisch Boundary value problem (kurz: BVP) nennt man in der Mathematik eine wichtige Klasse von Problemstellungen, in denen die Lösungen zu einer vorgegebenen Differentialgleichung (DGL) gesucht werden, die auf dem Rand des Definitionsbereiches vorgegebenene Funktionswerte (Randbedingung) annehmen sollen. Der Gegensatz dazu ist das Anfangswertproblem, bei dem nur Werte zu einem anfänglichen Zeitpunkt vorgegeben werden.

Beispiele/Definitionen

Gewöhnliche Differentialgleichung

Gesucht sind jeweils Lösungen $u:[a,b]\rightarrow\mathbb{R}$ (bzw. $u:[a,b]\rightarrow\mathbb{R}^n$ im mehrdimensionalen Fall)

nichtlinearer Fall

Im Eindimensionalen, d.h. $f:[a,b]\times\mathbb{R}^2\rightarrow\mathbb{R}$, besteht der Rand des Definitionsbereiches aus den Zahlen a und b. Ein nichtlineares RWP ist damit gegeben durch

$(N)\begin{cases} u''(x)=f(x,u(x),u'(x))& \\ u(a)=\eta_a,~u(b)=\eta_b.& \end{cases}$

Der mehrdimensionale nichtlineare Fall ist gegeben, falls $f:[a,b]\times\mathbb{R}^{2n}\rightarrow\mathbb{R}^n$ gilt.

Hinreichende Bedingungen zur Existenz von Lösungen von (N) liefern z. B. die Sätze von Scorza Dragoni, Nagumo oder Perov.

Sturm-Liouville-RWP

Seien $r,p,q\in\mathcal{C}([a,b],\mathbb{R})$
Lu: = (pu')' + qu sei ein selbstadjungierter linearer Differentialoperator 2. Ordnung
Randoperatoren mit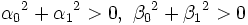 ${\alpha_0}^2+{\alpha_1}^2>0,~{\beta_0}^2+{\beta_1}^2>0$ seien
R_au: = α₀u(a) + α₁p(a)u'(a)
R_bu: = β₀u(b) + β₁p(b)u'(a)

$(*)\begin{cases} (Lu)(x)=r(x)& \\ R_u(a)=\eta_a,~R_u(b)=\eta_b& \end{cases}$

heißt Sturm-Liouville-RWP.

Sturm-Liouville-EWP (Eigenwertproblem)

$(P_\lambda)\begin{cases} (Lu)(x)=\lambda u(x)& \\ R_u(a)=R_u(b)=0& \end{cases}$

Diejenigen 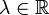$\lambda\in\mathbb{R}$, für die (P_λ) nicht eindeutig lösbar ist, heißen Eigenwerte. Die zugehörigen Lösungen heißen Eigenfunktionen.

Partielle Differentialgleichungen

Sei 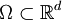$\Omega\subset\mathbb{R}^d$ offen und beschränkt, f sei eine auf Ω Lebesgue-messbare Funktion, g beschreibe die Randvorgaben. Gesucht sind jeweils Lösungen 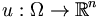$u:\Omega\rightarrow\mathbb{R}^n$. Die partielle Differentialgleichung sei gegeben durch den Differentialoperator 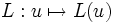$L:u \mapsto L(u)$. Insbesondere führen elliptische Differentialoperatoren immer auf Randwertprobleme, etwa der Laplace-Operator auf die Poisson-Gleichung.

Dirichlet-Problem

Beim Dirichlet-Problem werden Funktionswerte auf dem Rand vorgegeben.

L(u)(x) = f(x) für $x\in\Omega,$

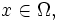
u(x) = g(x) für $x\in\partial\Omega$.

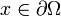Neumann-Problem

Anstatt Funktionswerten, werden beim Neumann-Problem Ableitungswerte vorgeschrieben.

L(u)(x) = f(x) für $x\in\Omega,$

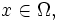
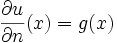$\frac{\partial u}{\partial n}(x)=g(x)$ für $x\in\partial\Omega$.

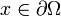Schiefe Randbedingung

Dies stellt eine Kombination der beiden vorangehenden Probleme dar. Hierbei soll die gesuchte Funktion auf dem Rand gleich ihrer Normalenableitung auf dem Rand sein.

L(u)(x) = f(x) für $x\in\Omega,$

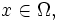
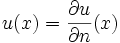$u(x)=\frac{\partial u}{\partial n}(x)$ für $x\in\partial\Omega$.

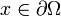Hilfsmittel

Ein wichtiges theoretisches Hilfsmittel zur Untersuchung von Randwertproblemen sind die Greenschen Funktionen.

In der Numerik werden als Verfahren zur näherungsweisen Lösung z.B. die FDM (finite difference method), die FEM (finite element method), das Schießverfahren und die Mehrzielmethode eingesetzt.

Naturwissenschaftliche Anwendung

Die Modellierung vieler Vorgänge in Natur und Technik baut auf Differentialgleichungen auf. Typische einfache Beispiele für RWP sind

• schwingende Saite, die an ihren beiden Enden(=Rand) fest eingespannt ist
• schwingende Membran (der Rand ist hier ein Kreisring)
• Bewegungsgleichungen von Satelliten bei Keplerbahnen, siehe auch Bahnbestimmung.

Literatur

• M. Hermann: Numerik gewöhnlicher Differentialgleichungen: Anfangs- und Randwertprobleme. Oldenbourg Verlag, München und Wien 2004. ISBN 3-486-27606-9