- Greibachnormalform
-
Die Greibach-Normalform ist ein Begriff der theoretischen Informatik, der im Zusammenhang mit kontextfreien Sprachen von Interesse ist. Sie ist nach der US-Informatikerin Sheila A. Greibach benannt und beschreibt eine Normalform der kontextfreien Grammatiken. Jede kontextfreie Grammatik, nach der nicht das leere Wort abgeleitet werden kann, kann in eine Greibach-Normalform transformiert werden. Die herausragende Eigenschaft der Greibach-Normalform ist, dass bei jedem Ableitungsschritt jeweils genau ein Terminalzeichen entsteht. Damit ist sie der natürliche Zwischenschritt bei der Umformung einer kontextfreien Grammatik in einen äquivalenten nichtdeterministischen Kellerautomaten ohne ε-Übergänge.
Eine weitere Normalform für kontextfreie Grammatiken ist die Chomsky-Normalform.
Inhaltsverzeichnis
Formale Definition
Sei G eine kontextfreie Grammatik (vgl. Chomsky-Hierarchie), also
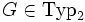 , mit
, mit 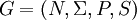 . Dabei sei N die Menge der Nichtterminalsymbole, Σ die Menge der Terminalsymbole, P die Menge von Produktionsregeln und S das Startsymbol. Sei das leere Element
. Dabei sei N die Menge der Nichtterminalsymbole, Σ die Menge der Terminalsymbole, P die Menge von Produktionsregeln und S das Startsymbol. Sei das leere Element 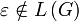 .
.G ist in Greibach-Normalform (kurz GNF), wenn alle Produktionen aus P die Form
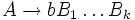 mit
mit 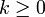 haben, wobei b ein Terminalsymbol ist und A und Bi für
haben, wobei b ein Terminalsymbol ist und A und Bi für 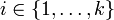 Nichtterminale sind. Mit
Nichtterminale sind. Mit 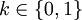 erhält man eine reguläre Grammatik als Spezialfall einer kontextfreien Grammatik in Greibach-Normalform.
erhält man eine reguläre Grammatik als Spezialfall einer kontextfreien Grammatik in Greibach-Normalform.Für alle
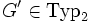 mit
mit 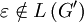 gibt es ein
gibt es ein 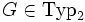 , mit
, mit 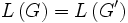 , in Greibach-Normalform.
, in Greibach-Normalform.Konstruktion der GNF
Ausgehend von der Chomsky-Normalform gibt es folgenden Algorithmus zur Überführung einer Grammatik in die Greibach-Normalform. Hierbei sind
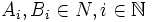 Nichtterminale,
Nichtterminale, 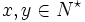 Folgen von Nichtterminalen,
Folgen von Nichtterminalen, 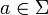 Terminale und
Terminale und 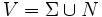 die Menge der Variablen.
die Menge der Variablen.Einsetzen der Produktionen
Gibt es eine Regel der Form
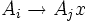 mit i > j, muss sie ersetzt werden.
mit i > j, muss sie ersetzt werden.Beispiel:
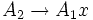 mit
mit 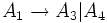 wird zu
wird zu 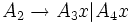 .
.Diese Ersetzung fangen wir beim höchsten i an und arbeiten uns bis zur 1 nach oben.
Ersetzen von linksrekursiven Regeln
Linksrekursive Regeln haben die Form
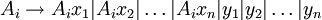 , d.h eine Variable kann wieder auf sich selbst ableiten. Durch den vorherigen Schritt des Algorithmus' ist gesichert, dass
, d.h eine Variable kann wieder auf sich selbst ableiten. Durch den vorherigen Schritt des Algorithmus' ist gesichert, dass 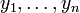 entweder mit einem Terminal oder einem
entweder mit einem Terminal oder einem 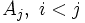 beginnen.
beginnen.Durch wiederholtes Einsetzen sieht man leicht, dass durch linksrekursive Regeln genau der Reguläre Ausdruck
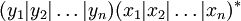
erzeugt werden kann. Dieser kann leicht simuliert werden:
Ersetze die Regeln für Ai mit: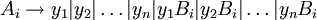
und füge neue Regeln für Bi ein:
 .
.Ab jetzt gibt es nur noch Regeln der Form
Entfernen der Regeln, die mit einem Nichtterminal beginnen
Jetzt können wir in allen Regeln, die zuerst auf ein Nichtterminal ableiten, die Produktionen dieses Nichtterminals einsetzen.
Ab jetzt gibt es nur noch Regeln der Form
 .
.Weiter bis Ende
Nun werden die Konstruktionsregeln auf alle Regeln von B analog angewandt.
Eine strengere Variante der Greibach-Normalform
Es ist auch möglich, die Produktionen einer kontextfreien Grammatik so in Greibach-Normalform umzuformen, dass auf den rechten Seiten maximal 2 Variablen vorkommen. Die resultierenden Produktionen haben dann also die Form
 ,
, 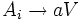 oder
oder 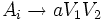 .
.Literatur
- Uwe Schöning: Theoretische Informatik kurzgefasst, 4. Auflage, Spektrum, ISBN 3827410991
Wikimedia Foundation.
