Grenzstabilität

Beispiel für eine mechanische Grenzstabilität

Der Begriff grenzstabil bzw. Grenzstabilität stammt aus der Stabilitätstheorie und bezeichnet ein System dessen Ausgangsgröße nicht ansteigt, aber auch nicht in einen stabilen Zustand übergeht. Ein Beispiel hierfür ist eine Dauerschwingung, deren Amplitude weder kleiner noch größer wird.

Ein stabiles System kehrt nach Störungen von selbst in seinen Ruhezustand zurück

Stabilität ist eine wichtige Eigenschaft von Systemen. Systeme können in instabile und stabile Systeme gegliedert werden. Entscheidend für die Einteilung sind die Eigenwerte der Systemmatrix A des Zustandsraummodell, die gleichzeitig auch die Wurzeln des charakteristischen Polynoms, sowie die Polstellen der Übertragungsfunktion darstellen.

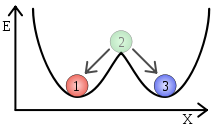
Grenzstabilität liegt vor, wenn sich Polstellen auf der Imaginärachse befinden, d.h. wenn der Realteil gleich Null ist.

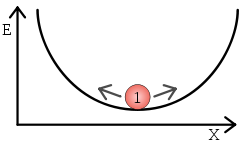
Ein System ist stabil, wenn alle Eigenwerte (bzw. Wurzeln bzw. Polstellen) einen negativen Realteil haben und damit in der linken Halbebene der komplexen Ebene (Pol-Nullstellen-Diagramm) liegen.

Der Zustand 2 ist instabil und geht ohne äußeren Einfluss in Zustand 1 oder 3 über.

Das System ist instabil, wenn mindestens einer dieser Realteile positiv ist und damit in der rechten Halbebene liegt.