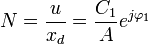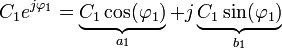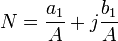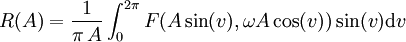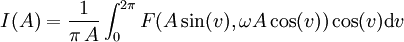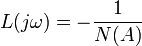Harmonische Linearisierung

Die Methode der harmonischen Balance ist ein Verfahren der Schwingungslehre um nachzuweisen, ob (nichtlinearen) Dauerschwingungen auftreten und ob diese stabil sind. In der Regelungstechnik wird es zu einem Verfahren zum Nachweis der Stabilität von nichtlinearen Systemen umgedeutet.

Die Auswertung kann sowohl algebraisch als auch graphisch erfolgen. In der graphischen Deutung zeigt sie Ähnlichkeit mit dem Stabilitätskriterium von Nyquist und dem Frequenzkennlinienverfahren, was die Anwendung vereinfacht. Es ist weiterhin unter den Begriffen Harmonische Linearisierung und Methode der Beschreibungsfunktion bekannt.

Harmonische Balance

Nichtlineares System im Zustand der harmonischen Balance

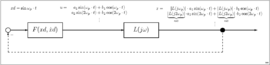
Das Verfahren geht von einem nichtlinearen Regelkreis, bestehend aus einem nichtlinearen Kennlinie und einem linearen Teil mit der Übertragungsfunktion L(jω) aus. Das lineare Teilsystem L(jω) sei stabil, habe höchstens einen Pol im Ursprung und Tiefpassverhalten.

Nach Krylow und Bogoljubow ^[1] spricht man vom Zustand der harmonischen Balance, wenn sich das System im Zustand einer Dauerschwingung mit der Frequenz 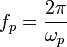$f_p=\frac{2\pi}{\omega_p}$ befindet. Es gelte

1. x_d eine sinusförmige Größe mit der Kreisfrequenz ω_p
2. dann ist u ebenfalls eine periodische Größe, die aus einer Grundschwingung mit der Frequenz ω_p und deren ganzzahlinge Vielfachen zusammengesetzt ist. Die einzelnen Amplituden lassen sich nach den Regeln der Fourierreihe bestimmen.
3. Hat nun L(jω) Tiefpassverhalten, so dass Frequenzen oberhalb ω_p gedämpft werden, so sind x und damit x_d sinusförmige Größen und Bedingung 1 ist erfüllt.

Damit brauchen auch die Vielfachen von ω_p in u nicht berücksichtigt werden. Damit ist die Nichtlinearität in System, dass eine Schwingung mit der Frequenz ω_p und der Amplitude A in eine phasenverschobene Schwingung mit gleicher Frequenz und anderer Amplitude überführt. Mit

x_d(t) = Ae^jωt

$u = C_1 e^{j (\omega t+ \varphi_1)}$

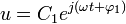
kann ein Ersatzfrequenzgang

$N = \frac{u}{x_d} = \frac{C_1}{A} e^{j \varphi_1}$

gebildet werden. Dabei ist

$C_1 e^{j \varphi_1}=\underbrace{C_1 \cos(\varphi_1)}_{a_1} + j \underbrace{C_1\sin(\varphi_1)}_{b_1}$

Es sind dabei a₁,b₁ die Grundwellenkoeffizienten von u bei Anregung mit x_d = Asin(ω_pt). Damit ist

$N = \frac{a_1}{A} + j\frac{b_1}{A}$

Für typische Nichtlinearitäten, bei denen F nur von x_d oder im Falle von Hysteresekurve vom Vorzeichen von 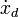$\dot x_d$ abhängt sind a₁,b₁ unabhängig von ω_p. Damit ist

N = N(A) = R(A) + jI(A)

und damit nur von der Amplitude nicht aber von der Frequenz abhängig.

N(A) wird als Beschreibungsfunktion bezeichnet. Da sie im Zustand der harmonischen Balance ähnlich einer Übertragungsfunktion die Kennlinie ersetzt wir auch von harmonischen Linearisierung gesprochen. Im Gegensatz zur Linearisierung gilt sie aber nur im Zustand der harmonischen Balance und aus Stetigkeitsgründen in deren Umgebung ^[2].

Der Zustand der harmonischen Bilanz wird durch

u₁ = N(A)x_d

− x_d = L(jω_p)u₁

also

(L(jω_p)N(A) + 1)x_d = 0

bzw. da es immer gelten soll

L(jω_p)N(A) + 1 = 0

Wenn der Zustand der harmonischen Balance existiert, erfüllen seine Amplitude A und ihre Kreisfrequenz ω_p vorstehende Gleichung.

Bestimmung der Beschreibungsfunktion

Der Realteil wird aus

$R(A) = \frac{1}{\pi\,A}\int_0^{2\pi} F(A \sin(v), \omega A \cos(v)) \sin(v) \textrm{d}v$

der Imaginärteil

$I(A) = \frac{1}{\pi\,A}\int_0^{2\pi} F(A \sin(v), \omega A \cos(v)) \cos(v) \textrm{d}v$

bestimmt.

Hängt die Nichtlinearität höchstens von 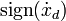$\textrm{sign}(\dot x_d)$ ab, ist also eine Hysteresekurve, so kann I(A) vereinfacht nach

$I(A) = \int_{-A}^{A} (F_o(x_d)-F_u(x_d)) \textrm{d}x_d$,

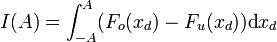wobei F_o(x_d) den oberen, F_u(x_d) unteren Zweig der Hysteresekurve beschreibt. I(A) ist also die eingeschlossene Fläche der Hysteresekurve und verschwindet, wenn die Nichtlinearität eindeutig ist.

Beispiele

Name	Bild	Beschreibungsfunktion N(A)	Nichtlineare Ortskurve 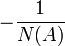$-\frac{1}{N(A)}$
Zweipunktglied	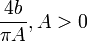	$\frac{4b}{\pi A}, A>0$
Begrenzung

Lösung der Gleichung der Harmonischen Balance

Um festzustellen, ob ein Grenzzyklus vorliegt oder nicht muss die Gleichung der harmonischen Balance

L(jω_p)N(A) + 1 = 0

gelöst werden. Dies ist einerseits algebraisch, anderseits geometrisch möglich

Algebraische Lösung

Es wird die komplexe Gleichung

N(A) = − L(jω_p) ^{− 1}

in den Real- und Imaginärteil

Re(N(A)) = − Re(L(jω_p) ^{− 1})

Im(N(A)) = − Im(L(jω_p) ^{− 1})

aufgeteilt. Der Lösungsweg vereinfacht sich, wenn die Kennlinie eindeutig ist und daher Im(N(A)) = 0 gilt. In diesem Fall kann zuerst aus der Gleichung für den Imaginärteil die Kreisfrequenz des Grenzzyklus und aus der Gleichung für den Realteil seine Amplitude bestimmt werden. Diese Rechnung vereinfacht sich, wenn L(jω) reines Verzögerungsverhalten hat und damit L(jω) ^{− 1} ein Polynom in ω ist.

Geometrische Lösung

Ausgangspunkt ist hier die Darstellung

$L(j\omega) = - \frac{1}{N(A)}$

die in die Ortskurven

z = L(jω) (bekannte Ortskurve der linearen Regelungstheorie)

und

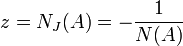$z = N_J(A) = - \frac{1}{N(A)}$ (nichtlineare Ortskurve ^[3])

aufgeteilt wird. Schneiden sich beide Kurven, so liegt eine nichtlineare Grenzschwingung vor. Für die Lösung im Bode-Diagramm sei auf ^[4] verwiesen.

Umdeutung als Stabilitätskriterium

Stabilität bedeutet im wesentlichen, dass Auslenkungen aus einer einmal erreichte Gleichgewichtslage nicht dazu führen, dass diese endgültig verlassen werden. Vor diesem Hintergrund können folgende Fälle unterschieden werden.

1. Die Trajektorie strebt einer neuen Gleichgewichtslage zu
2. Die Trajektorie strebt ins Unendliche
3. Die Trajektorie strebt mit der Zeit einer Kurve zu, die sei als Grenzkurve besitzt

Da der zweite Fall in realen Systemen wegen der Begrenzung aller Zustandsgrößen nicht möglich ist folgt aus dem Nichtvorhandensein einer Grenzkurve die Stabilität. Wenn die Gleichung der harmonischen Balance lösbar ist, ist die Gleichgewichtslage nicht stabil..^[5]

Literatur

• Otto Föllinger: Nichtlineare Regelungen, Bd. 1: Grundbegriffe, Anwendung der Zustandsebene, direkte Methode. 5. Auflage. Oldenbourg, München 1989, ISBN 3-486-21457-8.  (aktuell ist Auflage 8)

Einzelnachweise

Die Einzelnachweise beziehen sich Otto Föllinger, Nichtlineare Regelungen I, 5. Auflage, R. Oldenbourg Verlag München Wien

1. ↑ FOE, S. 71
2. ↑ FOE S. 79
3. ↑ FOE S. 90
4. ↑ FOE Kap. 5 S. 156ff
5. ↑ FOE, S. 69