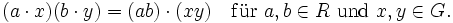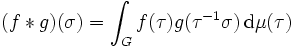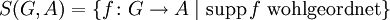Gruppenring

Ein Monoidring kann als Verallgemeinerung eines Polynomrings aufgefasst werden. Dabei werden die Exponenten (Hochzahlen) der Polynome sozusagen durch Elemente aus einem Monoid ersetzt, was im folgenden exakt definiert wird.

Definition

Sei R ein kommutativer Ring mit Eins und G ein Monoid, dann ist

$R[G]:=\{\alpha\colon G\to R {\big |} \alpha(x)=0$ für alle bis auf endlich viele x}

mit der Addition

(α + β)(x): = α(x) + β(x)

und der Faltung

(αβ)(z): =	∑	α(x)β(y)
	xy = z

als Multiplikation ein Ring. Die Konstruktion ist der des Polynomrings nachempfunden. Man schreibt 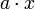$a \cdot x$ oder einfach ax für die Abbildung $\alpha \in R[G]$, die an der Stelle x den Wert a und ansonsten 0 annimmt. Beispielsweise gilt dann

$(a\cdot x)(b\cdot y) = (ab) \cdot (xy)\quad\mathrm{f\ddot ur}\ a,b\in R\ \mathrm{und}\ x,y\in G.$

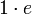R[G] besitzt ein Einselement, nämlich $1\cdot e$, wobei 1 das Einselement von R und e das Neutralelement von G ist.

Ist G eine Gruppe, so heißt R[G] Gruppenring oder Gruppenalgebra; auch die Schreibweise RG ist üblich.

R[G] wird zur R-Algebra via

r	∑	rigi: =	∑	rrigi
	i		i

Eigenschaften

• R[G] ist genau dann ein kommutativer Ring, wenn G als Monoid kommutativ ist.
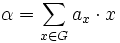• Jedes Element $\alpha \in R[G]$ lässt sich eindeutig schreiben als $\alpha=\sum_{x\in G} a_x\cdot x$ mit a_x: = α(x)
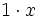• R und G sind auf natürliche Weise in R[G] eingebettet, nämlich durch die injektiven Ringhomomorphismen $f_0:R \to R[G],~f_0(r)=r\cdot e$ und $f_1: G\to R[G],~f_1(x)=1\cdot x$, wobei $1\cdot x$ wie oben definiert ist.
• Falls G ein Monoid ist und A,B kommutative Ringe, 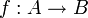$f:A\to B$ ein Ringhomomorphismus, dann gibt es einen eindeutigen Homomorphismus $h:A[G]\to B[G]$. sodass $h\left(\sum_{x\in G} a_x x\right)=\sum_{x\in G} f(a_x)x$

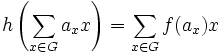
universelle Eigenschaft

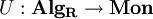Der Monoidring bzw. die Monoidalgebra kann auch - bis auf Isomorphie - über eine universelle Eigenschaft definiert werden. Seien G und R wie oben definiert. Es bezeichne $\mathbf{Mon}$ die Kategorie der Monoide und $\mathbf{Alg_R}$ die Kategorie der (assoziativen) R-Algebren. Sei $U: \mathbf{Alg_R} \to \mathbf{Mon}$ der Vergissfunktor, d.h. der Funktor, der jeder R-Algebra ihr multiplikatives Monoid zuordnet.

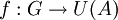Dann ist die kanonische Einbettung $\phi: G \to U(R[G]), g \mapsto 1g$ universell, d.h.: Falls wir noch einen anderen Monoid-Homomorphismus $f: G \to U(A)$ in das multiplikative Monoid einer R-Algebra A haben, dann existiert genau ein R-Algebra-Homomorphismus $\bar f: R[G] \to A$, so dass $U(\bar f) \circ \phi = f$.

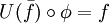In der obigen Konstruktion der Monoidalgebra sieht 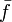$\bar f$ wie folgt aus: $\bar f (\sum_i r_i g_i) = \sum_i r_i f(g_i)$.

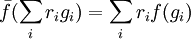Wenn wir den Funktor, der jedem Monoid seine Monoidalgebra über R zuordnet mit F bezeichnen, ist also F linksadjungiert zu U. So erhalten wir eine sehr kurze Definition der Monoidalgebra, jedoch muss man immer noch die Existenz beweisen.

Beispiele

• R[N₀] ist isomorph zum Polynomring in einer Unbestimmten über R.
• Ist allgemeiner G ein freies kommutatives Monoid in n Erzeugern, so ist R[G] isomorph zum Polynomring in n Unbestimmten über R.

Verallgemeinerungen

• Es sei G eine lokalkompakte topologische Gruppe. Ist G nicht diskret, so enthält der Gruppenring $\mathbb C[G]$ keine Information über die topologische Struktur von G. Deshalb nimmt seine Rolle die Faltungsalgebra der integrierbaren Funktionen ein: es sei μ ein linksinvariantes Haarmaß auf G. Dann bildet der Raum L¹(G,μ) mit der Faltung

$(f*g)(\sigma)=\int_G f(\tau)g(\tau^{-1}\sigma)\,\mathrm d\mu(\tau)$

als Produkt eine Banachalgebra.

• Ist A ein Ring und G eine totalgeordnete Gruppe, deren Ordnung kompatibel mit der Gruppenoperation ist, d.h.

aus α < β und γ < δ folgt αγ < βδ,

so sei

$S(G,A)=\{f\colon G\to A\mid\mathrm{supp}\,f\ \mathrm{wohlgeordnet}\}$

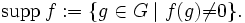mit $\mathrm{supp}\,f:=\{g\in G\mid f(g)\not=0\}.$ Mit der Faltung als Multiplikation und der komponentenweisen Addition wird S(G,A) zu einem Ring. Ist A ein Körper, so ist S(G,A) ein Schiefkörper. Ist beispielsweise 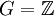$G=\mathbb Z$ mit der natürlichen Ordnung, so ist S(G,A) der Ring der formalen Laurentreihen mit Koeffizienten in A.

Literatur

• Serge Lang: Algebra, Graduate Texts in Mathematics, Revised Third Edition (Springer, 2002, ISBN 0-387-95385-X)