- Konvolution
-
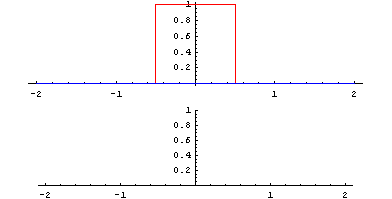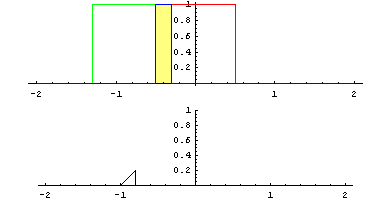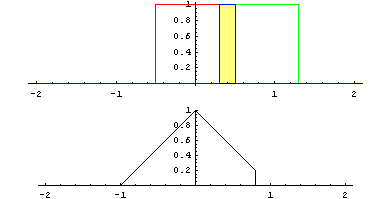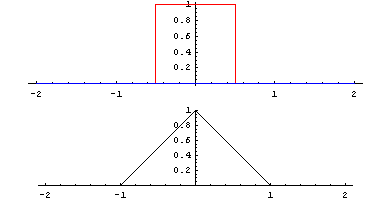
In der Mathematik und besonders in der Funktionalanalysis beschreibt die Faltung einen mathematischen Operator, der für zwei Funktionen f und g eine dritte Funktion liefert. Diese gibt eine Art „Überlappung“ zwischen f und einer gespiegelten und verschobenen Version von g an und ähnelt einem gleitenden Durchschnitt.
Inhaltsverzeichnis
Definition
Für zwei auf dem reellen Intervall D definierte Funktionen
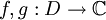 wird die Faltung von f mit g als f * g notiert. Sie ist als das Integral über dem Produkt von f mit einer am Ursprung gespiegelten und verschobenen Version von g definiert:
wird die Faltung von f mit g als f * g notiert. Sie ist als das Integral über dem Produkt von f mit einer am Ursprung gespiegelten und verschobenen Version von g definiert:Der Integrationsbereich ist der gesamte Definitionsbereich D beider Funktionen. Im Fall eines beschränkten Definitionsbereichs werden f und g oft als periodisch fortgesetzt angenommen, damit der Faktor g(t − τ) stets definiert ist. In diesem Fall wird die Faltungsoperation auch als zirkulare, zyklische oder periodische Faltung bezeichnet. Oder es werden f und g stattdessen durch Null fortgesetzt, wie dies bei der aperiodischen Faltung der Fall ist. In einer anderen Konvention, wie sie vor allem bei Physikern und Ingenieuren üblich ist, könnte man auch die Bedeutung von t und τ so verändern dass man die dort übliche Beziehung
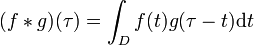 erhält, wobei τ der sog. Zeitversatz ist.
erhält, wobei τ der sog. Zeitversatz ist.Bedeutung
Eine anschauliche Deutung der Faltung ist die Gewichtung einer Funktion mit einer anderen. Der Funktionswert der Gewichtsfunktion f an einer Stelle τ gibt an, wie stark der um τ zurückliegende Wert der gewichteten Funktion, also g(t − τ), in den Wert der Ergebnisfunktion an der Stelle t eingeht.
Die Faltung ist ein geeignetes Modell zur Beschreibung zahlreicher physikalischer Vorgänge.
- Bei einem linearen, zeitinvarianten Übertragungsglied ergibt sich die Antwort auf eine Anregung durch Faltung der Anregungsfunktion mit der Impulsantwort des Übertragungsglieds. Beispielsweise stellt die lineare Filterung eines elektronischen Signals die Faltung der Original-Funktion mit der Impulsantwort dar.
- Bei optischen Abbildungen stellt das Bild die Faltung der originalen Bildfunktion mit der Punkt-Verbreiterungs-Funktion (Point Spread Function oder PSF) dar (Unschärfe).
- Diffusions-Prozesse lassen sich ebenfalls durch die Faltung beschreiben.
- Wenn X und Y zwei stochastisch unabhängige Zufallsvariablen mit den Wahrscheinlichkeitsdichten f und g sind, dann ist die Dichte der Summe X+Y gleich der Faltung f * g.
Diskrete Faltung
In der digitalen Signalverarbeitung und der digitalen Bildverarbeitung hat man es meist mit diskreten Funktionen zu tun. Hier seien die Funktionen
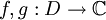 gegeben. Dabei ist der Definitionsbereich
gegeben. Dabei ist der Definitionsbereich 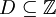 .
.Die diskrete Faltung ist definiert als:
Der Summationsbereich ist der gesamte Definitionsbereich D beider Funktionen. Im Fall eines beschränkten Definitionsbereichs werden f und g meist durch Null fortgesetzt.
Das Produkt zweier Polynome f und g ist z.B. die diskrete Faltung ihrer mit Nullen fortgesetzten Koeffizientenfolgen. Die dabei auftretenden unendlichen Reihen haben stets nur endlich viele Summanden, die ungleich Null sind. Analog definiert man das Produkt zweier formaler Laurentreihen mit endlichem Hauptteil.
Ein in Bezug auf die Rechenleistung effizienter Algorithmus für die Berechnung der diskreten Faltung ist die Schnelle Faltung, die sich ihrerseits auf die Schnelle Fourier-Transformation (FFT) zur effizienten Berechnung der diskreten Fourier-Transformation stützt.
Eine interaktive Visualisierung als Java-Applet ist hierzu zu finden unter [1].
Glättungskern
Eine schöne Methode, eine Funktion f zu „glätten“, besteht darin, sie mit einem so genannten Glättungskern zu falten. Die entstehende Funktion F ist glatt (unendlich oft stetig differenzierbar), ihr Träger ist nur etwas größer als der von f, und die Abweichung in der L1-Norm lässt sich durch eine vorgegebene positive Konstante beschränken.
Ein d-dimensionaler Glättungskern (engl. mollifier) ist eine unendlich oft stetig differenzierbare Funktion
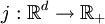 , die nichtnegativ ist, ihren Träger in der abgeschlossenen Einheitskugel B(0, 1) hat und das Integral 1, durch entsprechende Wahl einer Konstanten c, besitzt.
, die nichtnegativ ist, ihren Träger in der abgeschlossenen Einheitskugel B(0, 1) hat und das Integral 1, durch entsprechende Wahl einer Konstanten c, besitzt.Ein Beispiel ist der Glättungskern
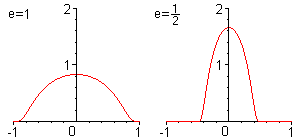
Aus dieser Funktion kann man weitere Glättungskerne bilden, indem man für e eine Zahl zwischen 0 und 1 setzt:
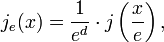 wobei je(x) = 0 für | x | > e.
wobei je(x) = 0 für | x | > e.
Beispiele
Sei
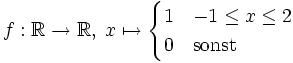 .
.
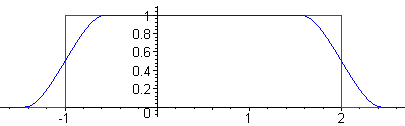
Durch Faltung von f (rot dargestellt) mit dem Glättungskern j1 / 2 entsteht eine glatte Funktion F = f * j1 / 2 (blau dargestellt) mit kompaktem Träger, die von f in der L1-Norm um etwa 0,4 abweicht, d.h.
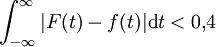 .
.
Bei der Faltung mit je für e kleiner 1/2 erhält man glatte Funktionen, die in der Integralnorm noch dichter bei f liegen.
Eigenschaften der Faltung; Faltungstheorem
Von den folgenden Aussagen ist das sog. Faltungstheorem wegen seiner vielfältigen Anwendungen besonders wichtig:
- Assoziativität mit der skalaren Multiplikation
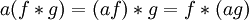
- Wobei a eine beliebige komplexe Zahl ist.
- Faltungstheorem
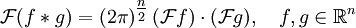
- Wobei
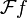 die Fouriertransformierte von f beschreibt. Ein ähnliches Theorem gilt auch für die Laplacetransformation.
die Fouriertransformierte von f beschreibt. Ein ähnliches Theorem gilt auch für die Laplacetransformation.
- Ableitungsregel
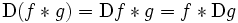
- Dabei ist Df die Ableitung f' von f bzw. im diskreten Fall die Differenz Df(n) = f(n + 1) − f(n).
- Faltung mit speziellen Funktionen
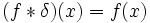 , wobei δ die Delta-Distribution ist. δ ist also das neutrale Element der Faltung.
, wobei δ die Delta-Distribution ist. δ ist also das neutrale Element der Faltung.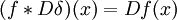 , wobei Dδ die Ableitung der Delta-Distribution ist. Die Ableitung lässt sich also als Faltungsoperator auffassen.
, wobei Dδ die Ableitung der Delta-Distribution ist. Die Ableitung lässt sich also als Faltungsoperator auffassen.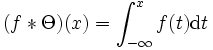 , wobei Θ die Sprungfunktion ist.
, wobei Θ die Sprungfunktion ist.
- Faltungsalgebra
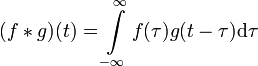
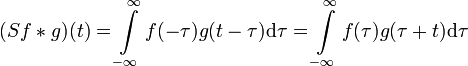 , wobei S der Spiegelungsoperator mit Sf(t) = f( − t) für alle t ist.
, wobei S der Spiegelungsoperator mit Sf(t) = f( − t) für alle t ist.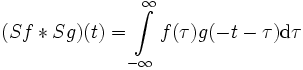
Verallgemeinerungen
Die beiden Faltungsbegriffe können gemeinsam beschrieben und verallgemeinert werden durch einen allgemeinen Faltungsbegriff für komplexwertige m-integrierbare Funktionen auf einer geeigneten topologischen Gruppe G mit einem Maß m (z. B. einer lokalkompakten hausdorffschen topologischen Gruppe mit einem Haar-Maß):
Dieser Faltungsbegriff spielt eine zentrale Rolle in der Darstellungstheorie dieser Gruppen, deren wichtigste Vertreter die Liegruppen bilden. Die Algebra der integrierbaren Funktionen mit dem Faltungsprodukt ist für kompakte Gruppen das Analogon zum Gruppenring einer endlichen Gruppe. Weiterführende Themen sind:
- Satz von Peter-Weyl
- Harmonische Analyse
Eine andere Verallgemeinerung ist die Faltung von Distributionen,
wobei τx die Verschiebung um x nach links bezeichnet.
Anwendung
- In der Optik können verschiedenste Bildstörungen als Faltung des Originalbildes mit einem entsprechenden Kern modelliert werden. In der digitalen Bildbearbeitung wird die Faltung daher benutzt, um solche Effekte zu simulieren. Auch andere digitale Effekte beruhen auf der Faltung.
- In der Akustik (Musik) wird die Faltung (unter Zuhilfenahme der FFT = schnelle Fouriertransformation) auch zur digitalen Erzeugung von Hall und Echos und zur Anpassung von Klangeigenschaften verwendet. Dazu wird die Impulsantwort des Raumes, dessen Klangcharakteristik man übernehmen möchte, mit dem Signal, das man beeinflussen möchte, gefaltet.
- In der Ingenieurmathematik und der Signalverarbeitung werden Eingangssignale (äußere Einflüsse) mit der Übertragungsfunktion (= Impulsantwort = Reaktion des betrachteten Systems auf einen Diracimpuls als Signaleingang) gefaltet, um die Antwort eines LTI-Systems auf beliebige Eingangssignale zu berechnen. Die Übertragungsfunktion ist nicht zu verwechseln mit der Übergangsfunktion. Erstere beschreibt die Gesamtheit aus System und einem Dirac-Impuls als Eingangs-Testfunktion, letztere die Gesamtheit aus System und einer Sprungfunktion als Eingangs-Testfunktion. Die Berechnungen finden meist nicht im Zeitbereich, sondern im Frequenzbereich statt. Dazu müssen sowohl das Signal als auch die das Systemverhalten beschreibende Übertragungsfunktion im Frequenzbereich vorliegen, oder ggf. aus dem Zeitbereich per Fouriertransformation oder einseitiger Laplacetransformation dorthin transformiert werden.
- In der numerischen Mathematik erhält man durch Faltung der Boxfunktion N0(t) mit Nk − 1(t) die B-Spline Basisfunktion Nk(t) für den Vektorraum der stückweisen Polynome vom Grad k.
- Ebenfalls in der numerischen Mathematik kann die Faltung für eine effiziente Berechnung der Multiplikation vielstelliger Zahlen eingesetzt werden, da die Multiplikation im wesentlichen eine Faltung mit nachfolgendem Übertrag darstellt. Die Komplexität dieses Vorgehens ist mit
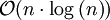 nahe linear, während das „Schulverfahren“ quadratischen Aufwand
nahe linear, während das „Schulverfahren“ quadratischen Aufwand 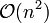 hat, wobei n die Zahl der Stellen ist. Dies lohnt sich trotz des zusätzlichen Aufwands, der hierbei für die Fouriertransformation (und deren Umkehrung) erforderlich ist.
hat, wobei n die Zahl der Stellen ist. Dies lohnt sich trotz des zusätzlichen Aufwands, der hierbei für die Fouriertransformation (und deren Umkehrung) erforderlich ist.
Literatur
- Bourbaki: Integration
- Kôsaku Yosida: Functional Analysis. Springer-Verlag, ISBN 3-540-58654-7.
Weblinks
Wikimedia Foundation.

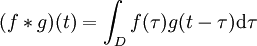
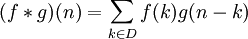
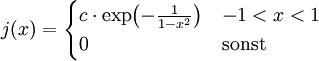
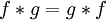
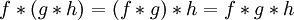
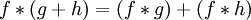
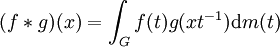
![(T * \varphi)(x) := T[\tau_x \varphi],](/pictures/dewiki/98/b6fdded21f0da3b0d43df99b5d9d72d5.png)