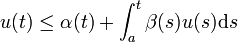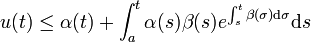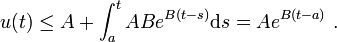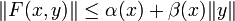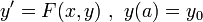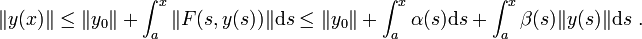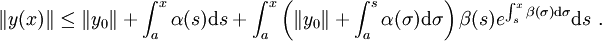Grönwallsche Ungleichung

Die grönwallsche Ungleichung ist eine Ungleichung, die es erlaubt, aus der impliziten Information einer Integralungleichung explizite Schranken herzuleiten. Des Weiteren ist sie ein wichtiges Hilfsmittel zum Beweis von Existenz- und Einschließungssätzen für Lösungen von Differential- und Integralgleichungen. Sie ist nach Thomas Hakon Grönwall benannt, der sie im Jahr 1919 bewies und in einer wissenschaftlichen Veröffentlichung beschrieb.

Formulierung

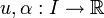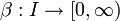Gegeben seien ein Intervall $\ I := [a, b]$ sowie stetige Funktionen $u, \alpha: I \rightarrow \mathbb{R}$ und $\beta: I \rightarrow [0, \infty)$. Weiter gelte die Integralungleichung

$u(t) \leq \alpha(t) + \int_a^t \beta(s)u(s){\rm d}s$

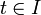für alle $t \in I$. Dann gilt die grönwallsche Ungleichung

$u(t) \leq \alpha(t) + \int_a^t\alpha(s)\beta(s)e^{\int_s^t\beta(\sigma){\rm d}\sigma}{\rm d}s$

für alle $t\in I$.

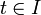Spezialfall

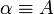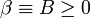Im Fall konstanter Funktionen $\alpha \equiv A$ und $\beta \equiv B \geq 0$ lautet die grönwallsche Ungleichung

$u(t) \leq A + \int_a^tABe^{B(t-s)}{\rm d}s = Ae^{B(t-a)}\ .$

Anwendungen

Eindeutigkeitssatz für Anfangswertprobleme

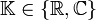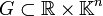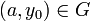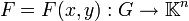Es sei $\mathbb{K} \in \{\mathbb{R}, \mathbb{C}\}$, $G \subset \mathbb{R} \times \mathbb{K}^n$, $(a, y_0) \in G$ und $F = F(x,y): G \rightarrow \mathbb{K}^n$ stetig sowie lokal Lipschitz-stetig bezüglich der zweiten Variablen. Dann besitzt das Anfangswertproblem 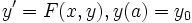$\ y' = F(x,y), y(a) = y_0$ höchstens eine Lösung $y \in C^1([a, b); \mathbb{K}^n)$.

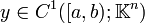Linear beschränkte Differentialgleichungen

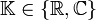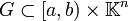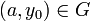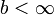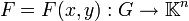Seien $\mathbb{K} \in \{\mathbb{R}, \mathbb{C}\}$, $G \subset [a,b) \times \mathbb{K}^n$, $(a,y_0) \in G$, $b < \infty$ und $F = F(x,y): G \rightarrow \mathbb{K}^n$ stetig. Weiter gebe es Funktionen 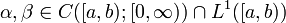$\alpha,\beta \in C([a,b); [0, \infty)) \cap L^1([a,b))$ derart, dass

$\|F(x,y)\| \leq \alpha(x) + \beta(x)\|y\|$

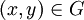für alle $(x,y) \in G$. Dann gilt für jede Lösung y von

$y'=F(x,y)\ ,\ y(a) = y_0$

auf [a,b), dass y beschränkt ist.

Beweis

Es gilt

$\|y(x)\| \leq \|y_0\| + \int_a^x\|F(s,y(s))\|{\rm d}s \leq \|y_0\| + \int_a^x\alpha(s){\rm d}s + \int_a^x\beta(s)\|y(s)\|{\rm d}s\ .$

Die grönwallsche Ungleichung impliziert

$\|y(x)\| \leq \|y_0\| + \int_a^x\alpha(s){\rm d}s + \int_a^x\left(\|y_0\| + \int_a^s\alpha(\sigma){\rm d}\sigma\right)\beta(s)e^{\int_s^x\beta(\sigma){\rm d}\sigma}{\rm d}s\ .$

$\Box$

Weblinks

• Beweis der grönwallschen Ungleichung im Beweisarchiv
• Anwendung der grönwallschen Ungleichung für den Eindeutigkeitssatz von Anfangswertproblemen bei lokal Lipschitz-stetiger Differentialgleichung
• Die grönwallsche Ungleichung auf planetmath.org

Literatur

• Herbert Amann: Gewöhnliche Differentialgleichungen. 2. Auflage. Gruyter - de Gruyter Lehrbücher, Berlin/New York 1995, ISBN 3-11-014582-0.