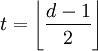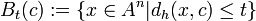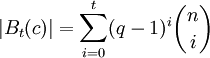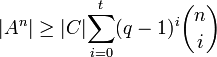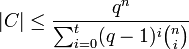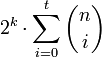- Hamming-Schranke
-
Ein perfekter Code, oder auch dicht gepackter Code, bezeichnet in der Codierungstheorie einen Blockcode
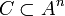 , bei dem jedes Wort
, bei dem jedes Wort 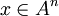 nur zu genau einem Codewort
nur zu genau einem Codewort 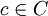 eine minimale Hamming-Distanz hat.
eine minimale Hamming-Distanz hat.Bei der für gewöhnlich verwendeten Maximum-Likehood Decodierung bedeutet dies, dass jedem empfangenen Wort ein Codewort eindeutig zugeordnet werden kann. Daraus leitet sich die Bezeichnung perfekt ab, denn es gibt keine mehrdeutigen Decodiermöglichkeiten.
Inhaltsverzeichnis
Mathematische Beschreibung
Sei
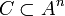 ein Blockcode mit | A | = q, wobei A das verwendete Alphabet darstellt. C habe eine Hammingdistanz von d. Er kann damit
ein Blockcode mit | A | = q, wobei A das verwendete Alphabet darstellt. C habe eine Hammingdistanz von d. Er kann damitFehler korrigieren.
Um perfekt zu sein, muss ein Code also eine ungerade Hammingsdistanz haben, da es sonst für
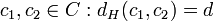 ein Wort x mit
ein Wort x mit 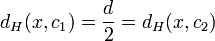 gibt, was im Widerspruch zur Definition eines perfekten Codes steht.
gibt, was im Widerspruch zur Definition eines perfekten Codes steht.Da der Code t fehlerkorrigierend ist, kann ein Wort
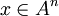 einem Codewort
einem Codewort 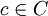 eindeutig zugeordnet werden, wenn die Hammingdistanz
eindeutig zugeordnet werden, wenn die Hammingdistanz 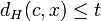 ist. Umgekehrt bedeutet dies für ein bestimmtes Codewort c, dass alle Wörter x mit einer Hammingdistanz von höchstens t nach c decodiert werden. Als Menge wird dies so geschrieben:
ist. Umgekehrt bedeutet dies für ein bestimmtes Codewort c, dass alle Wörter x mit einer Hammingdistanz von höchstens t nach c decodiert werden. Als Menge wird dies so geschrieben:Diese Menge wird auch als Kugel (manchmal auch Hyperwürfel) mit Radius t um c bezeichnet. Die Anzahl der Elemente von Bt(c) ist dabei:
Für i Fehlerstellen gibt es i aus n mögliche Positionen für die Fehler. Dabei stehen pro Fehlerstelle q − 1 falsche Symbole zur Verfügung. Es gibt | C | Kugeln. Diese sind disjunkte Teilmengen des An. Daraus ergibt sich die Ungleichung
Aufgelöst nach C und mit | An | = qn folgt:
Diese Ungleichung für die Anzahl der Codewörter wird Hammingschranke oder auch Kugelpackungsschranke genannt.
Bei einem perfekten Code sind alle Wörter
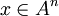 in einem der Bälle enthalten (anders ausgedrückt: Die Bälle überdecken den Raum). Deshalb gilt bei der Hammingschranke für diesen Code dann die Gleichheit.
in einem der Bälle enthalten (anders ausgedrückt: Die Bälle überdecken den Raum). Deshalb gilt bei der Hammingschranke für diesen Code dann die Gleichheit.Alternative Interpretation
Man kann sich diese Grenze auch wie folgt veranschaulichen (der Einfachheit halber nur anhand binärer Codes erläutert, d.h. für q = 2):
Für einen t Fehler korrigierenden Code muss der Decoder genug Information erhalten, um alle folgenden Fälle unterscheiden zu können:
- | C | = 2k verschiedene Informationswörter und jeweils
- alle möglichen Muster von
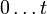 Bitfehlern der n Bits eines Codewortes
Bitfehlern der n Bits eines Codewortes
Da es
 Möglichkeiten gibt, i Bitfehler auf n Bits zu verteilen, ergeben sich insgesamt
Möglichkeiten gibt, i Bitfehler auf n Bits zu verteilen, ergeben sich insgesamtFälle, die mit den zur Verfügung stehenden n Bits unterschieden werden müssen, also
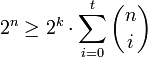 .
.
Bei einem perfekten Code gilt Gleichheit, d.h. die n Bits tragen exakt die minimal benötigte Information. Diese (Un)Gleichung entspricht der obigen allgemeinen Definition für den Fall q = 2 und | C | = 2k.
Es sei noch angemerkt, dass man zwar eigentlich nur an der Korrektur der k Informationsbits interessiert ist, wofür entsprechend weniger Zusatzinformation genügte, dass diese n − k Bits Zusatzinformation dann aber fehlerfrei sein müssten, was natürlich i.d.R. nicht gewährleistet werden kann. Daher ist eine Korrektur aller n Bits erforderlich.
Bekannte Perfekte Codes
Es gibt - bis auf Isomorphie – lediglich die folgenden perfekten Codes: [1][2]
- Alle trivialen Codes beliebiger Länge: Codes die nur aus einem Codewort bestehen.
- Binäre Wiederholungs-Codes mit ungerader Codewortlänge.
- Alle binären Hamming-Codes. Hamming-Codes können nur Einfachfehler erkennen und korrigieren. Alle Mehrfachfehler in einem Codewort führen zu Decodierversagen.
- Der binäre Golay-Code (23,12,7) G23.
- Die beiden ternären Golay-Codes (11,6,5) G11 und (23,11,5) G23 über dem Galois-Körper GF(3).
Einzelnachweise
Wikimedia Foundation.