- Hamming-Gewicht
-
Der Hamming-Abstand, die Hamming-Distanz und das Hamming-Gewicht, benannt nach dem US-amerikanischen Mathematiker Richard Wesley Hamming (1915–1998), sind Maße für die Unterschiedlichkeit von Zeichenketten. Häufig handelt es sich um binär dargestellte Zahlen, so zum Beispiel in der Kodierungstheorie, für andere Zahlensysteme oder Alphabete existieren jedoch ebenfalls wichtige Anwendungen.
Der Hamming-Abstand zweier Blöcke von binären Daten mit fester Länge (so genannter Codewörter) kann ermittelt werden, indem man beide in binärer Form schreibt, diese Bit für Bit vergleicht und die Stellen zählt, die ungleich sind. Rechnerisch lässt sich der Vergleich durch eine XOR-Operation und das Abzählen der resultierenden Einsen realisieren.
Inhaltsverzeichnis
Definition
Sei Σ ein endliches Alphabet,
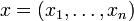 und
und 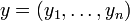 aus Σn, d.h. die einzelnen Komponenten sind aus Σ. Dann definiert man den Hammingabstand zwischen x und y als
aus Σn, d.h. die einzelnen Komponenten sind aus Σ. Dann definiert man den Hammingabstand zwischen x und y als 
Beispiel
- x = 00110
- y = 00100
- Der Hamming-Abstand ist hier 1, da sich die beiden Wörter x und y an genau einer Stelle (nämlich der vorletzten) unterscheiden.
Hamming-Gewicht
Das Hamming Gewicht eines Vektors ist definiert als:
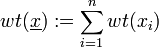 mit
mit 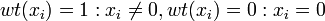 für
für 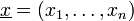
Anschaulich ist dies der Abstand zum Nullvektor und ist im binären Fall gleichbedeutend mit der Anzahl der gesetzten Bits.
Beispiel:
- x = 1011
- Das Hamming-Gewicht ist hier 3.
Ermitteln des Gewichts
In der Programmiersprache C kann das Hamming-Gewicht eines 8-Bit-Wortes wie folgt ermittelt werden:
unsigned int hamming_weight(unsigned char word) { unsigned int weight=0; for(int i = 0 ; i < 8; i++ ) { if( word & ( 1 << i ) ) { weight++; } } return weight; }
Hamming-Abstand eines Codes
Unter dem Hamming-Abstand eines kompletten Codes versteht man das Minimum aller Abstände zwischen Wörtern innerhalb des Codes.
Beispiel:
- Ein Code besteht aus folgenden drei Wörtern:
- x = 00110,
- y = 00101,
- z = 01110.
- Der Hamming-Abstand zwischen x und y ist 2.
- Um y zu generieren muß man zwei Bits (von rechts nach links das erste und zweite Bit) ändern: y = x XOR 00011.
- Der Hamming-Abstand zwischen x und z ist 1.
- Um z zu generieren muß man ein Bit (das vierte) ändern: z = x XOR 01000.
- Der Hamming-Abstand zwischen y und z ist 3.
- Um z zu generieren muß man drei Bits ändern: z = y XOR 01011.
Der kleinste der drei Abstände ist 1, also ist der Hamming-Abstand des Codes ebenfalls gleich 1.
Wichtig ist die Hamming-Distanz, wenn man Codes entwickeln möchte, die Fehlererkennung (EDC) oder -korrektur (ECC) ermöglichen. Bei Codes mit Hamming-Abstand h können alle (h-1)-Bit-Fehler erkannt werden. In dem Beispiel mit h = 1 kann somit nicht einmal jeder 1-Bit-Fehler erkannt werden (x↔z fällt nicht auf, alle anderen 1-Bit-Fehler erzeugen ungültige Codes, z.B. 00111 aus x oder y). Bei h = 2 können alle 1-Bit-Fehler erkannt werden. Um die Fehler auch korrigieren zu können, muss die Hamming-Distanz auf mindestens 2r+1 vergrößert werden, wobei r für die Anzahl der korrigierbaren Bit-Fehler steht.
Bei h = 3 können alle 1-Bit-Fehler erkannt und korrigiert werden. Treten 2-Bit-Fehler auf, werden diese unter Umständen falsch „korrigiert“, da das fehlerhafte Wort möglicherweise den Abstand 1 zu einem anderen gültigen Codewort hat.
Bei h = 4 können ebenfalls alle 1-Bit-Fehler erkannt und korrigiert werden. Treten 2-Bit-Fehler auf, können diese zwar erkannt, aber nicht mehr korrigiert werden. Eine falsche „Korrektur“ ist ab 3-Bit-Fehlern möglich.
Der Hamming-Abstand eines Codes ist notwendigerweise eine natürliche Zahl. Ein Code mit Hamming-Abstand 0 ist nicht möglich, da sich in diesem Fall zwei Codewörter nicht unterscheiden ließen.
Erzeugung von Hamming-Codes
Hammingcodes kann man durch einen Algorithmus erzeugen, der ähnlich dem Sieb des Eratosthenes für Primzahlen funktioniert. Um etwa alle Hammingcodes in einem 16-Bit Wort zu finden, die mindestens den Abstand 5 zueinander haben, beginnt man mit dem Wort '0000 0000 0000 0000'. Danach wird aufsteigend das nächste Wort gesucht, das zu dem bisherigen den Abstand 5 hat. Dies ist '0000 0000 0001 1111'.
Nun sucht man weiter nach dem dritten Wort, das zu ersten beiden Einträgen den Abstand 5 hat, und findet '0000 0000 0110 0011'. Fährt man fort, erhält man alle 256 Codewörter, die mit 16 Bits und Abstand 5 möglich sind.
Bit Distanz Hammingcodes Erkennbare Fehler Korrigierbare Fehler 6 3 8 2-Bitfehler 1-Bitfehler 7 3 16 2-Bitfehler 1-Bitfehler 8 3 16 2-Bitfehler 1-Bitfehler 8 4 16 3-Bitfehler 1-Bitfehler 12 3 256 2-Bitfehler 1-Bitfehler 12 4 128 3-Bitfehler 1-Bitfehler 12 5 16 4-Bitfehler 2-Bitfehler 12 6 16 5-Bitfehler 2-Bitfehler 16 3 2048 2-Bitfehler 1-Bitfehler 16 4 2048 3-Bitfehler 1-Bitfehler 16 5 256 4-Bitfehler 2-Bitfehler 16 6 128 5-Bitfehler 2-Bitfehler 16 7 32 6-Bitfehler 3-Bitfehler 16 8 32 7-Bitfehler 3-Bitfehler Repräsentation der Bit-Strings in einem Hyperwürfel
Die Idee der Hamming-Distanz kann gut mit Hilfe von Hyperwürfeln dargestellt werden. Ein Hyperwürfel ist die Generalisierung eines dreidimensionalen Würfels auf die Dimension d. Jeder Knoten der Figur entspricht einer Bitkombination, die auch als Koordinatenangabe im Raum verstanden werden kann. Die minimale Anzahl der Kanten, die traversiert werden müssen, um von einem gültigen Wort eines Codes zu einem anderen gültigen Wort des Codes zu gelangen, entspricht der Hamming-Distanz.
Beispiel
Wenn im nebenstehenden Würfel mit d = 3 die beiden Worte {101, 010} für einen Code gewählt werden, so beträgt die minimale Hamming-Distanz 3. Damit können in einer Sphäre mit dem Abstand 1 um einen Punkt mit einem gültigen Wort (z.B. für das gültige Code-Wort 010) alle Fehler (1-Bit-Fehler) erkannt und korrigiert werden {000, 110, 011}.
Wird ein Code mit den Worten {000, 101, 110, 011} gewählt, so beträgt die minimale Hamming-Distanz 2. Mit einem Hamming-Abstand von 2 lassen sich 1-Bit-Fehler lediglich erkennen, aber nicht korrigieren (beispielsweise lässt sich zwar erkennen, dass 111 ein fehlerhaftes Wort darstellt, jedoch nicht, ob es nach 110 oder 011 oder 101 korrigiert werden soll).
Mindestdistanz
Die Mindestdistanz zwischen zwei benachbarten Codewörtern ist für die Konstruktion eines Codes interessant, der bei m Bitstellen für Nutzinformation k Fehler korrigieren kann. Bei Blockcodes mit fixiertem Alphabet liefern die Singleton-Schranke, die Hamming-Schranke (Stichwort t-perfekt) und die Plotkin-Schranke allgemeinere Aussagen über den maximalen Minimalabstand.
Es gilt für einen Code mit Mindestabstand h, dass
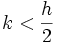 Fehler korrigierbar und h − 1 Fehler erkennbar sind.
Fehler korrigierbar und h − 1 Fehler erkennbar sind.Beispiel
Sollen alle Einzelfehler korrigierbar sein, also k = 1, so folgt durch Einsetzen und Umstellen h > 2. Mit h = 3 kann man 2-Bit-Fehler zwar erkennen, aber nur Einzelfehler auch korrigieren.
Folgerung
Bei jedem Code muss die Hammingdistanz h somit mindestens 3 betragen, damit überhaupt Fehler korrigierbar sind.
Siehe auch: Hamming-Ähnlichkeit, Hamming-Code, Levenshtein-Distanz
Literatur
Weblinks
Wikimedia Foundation.

