- Galois-Körper
-
Ein endlicher Körper oder Galoiskörper ist eine Menge mit einer endlichen Anzahl von Elementen, auf der die Grundoperationen Addition, Subtraktion, Multiplikation und Division definiert sind. Die Bezeichnung Galoiskörper leitet sich vom Namen des Mathematikers Évariste Galois ab, der als erster mit solchen Strukturen gerechnet hat.
Endliche Körper spielen eine wichtige Rolle in der Kryptographie und der Codierungstheorie (Vorwärtsfehlerkorrektur, zum Beispiel Reed-Solomon-Code).
Inhaltsverzeichnis
Katalog
Zu jedem Körper K gibt es einen eindeutig bestimmten unitären Ringhomomorphismus
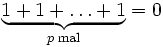
Ist K endlich, so kann die Abbildung nicht injektiv sein, somit gibt es eine kleinste positive ganze Zahl im Kern, d. h. eine Zahl p, so dass in K
gilt. Man kann zeigen, dass p eine Primzahl sein muss. Man nennt sie die Charakteristik von K.
Für jede Primzahl p ist der Restklassenring
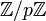 ein Körper der Charakteristik p und wird mit dem Symbol
ein Körper der Charakteristik p und wird mit dem Symbol 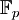 bezeichnet. Alternativ existiert die Schreibweise GF(p) (vom englischen Galois field).
bezeichnet. Alternativ existiert die Schreibweise GF(p) (vom englischen Galois field).Jeder endliche Körper der Charakteristik p enthält
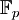 (bzw. eine isomorphe Kopie desselben) als Unterkörper. Er ist damit insbesondere ein Vektorraum über
(bzw. eine isomorphe Kopie desselben) als Unterkörper. Er ist damit insbesondere ein Vektorraum über 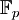 und als solcher isomorph zu
und als solcher isomorph zu 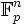 für eine natürliche Zahl n. Damit enthält er genau pn Elemente. Man kann zeigen, dass es bis auf Isomorphie genau einen Körper mit q = pn Elementen gibt; dieser wird dann mit
für eine natürliche Zahl n. Damit enthält er genau pn Elemente. Man kann zeigen, dass es bis auf Isomorphie genau einen Körper mit q = pn Elementen gibt; dieser wird dann mit 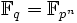 bezeichnet (veraltete Alternativschreibweise GF(pn)).
bezeichnet (veraltete Alternativschreibweise GF(pn)).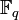 ist stets eine einfache Erweiterung von
ist stets eine einfache Erweiterung von 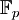 , d. h. es gibt ein irreduzibles Polynom
, d. h. es gibt ein irreduzibles Polynom ![f\in\mathbb F_p[X]](/pictures/dewiki/52/4252650903e0f71456ff63351028c58d.png) vom Grad n, so dass
vom Grad n, so dass ![\mathbb F_q\cong\mathbb F_p[X]/(f)](/pictures/dewiki/97/ae6de93d8babfe6e0f27f0384892b978.png) ist. Derartig irreduzible Polynome sind stets Faktoren von Xq − X, vergleiche Adjunktion (Algebra).
ist. Derartig irreduzible Polynome sind stets Faktoren von Xq − X, vergleiche Adjunktion (Algebra).Beispiele
Charakteristik 2
Im Restklassenkörper
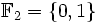 der ganzen Zahlen modulo 2 gilt 1 + 1 = 0. Die Verknüpfungstabellen sehen so aus:
der ganzen Zahlen modulo 2 gilt 1 + 1 = 0. Die Verknüpfungstabellen sehen so aus:Addition: + 0 1 0 0 1 1 1 0 Multiplikation: * 0 1 0 0 0 1 0 1 Das Polynom f = T2 + T + 1 ist irreduzibel über
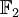 . Der Körper
. Der Körper ![\mathbb F_4\cong\mathbb F_2[T]/(f)](/pictures/dewiki/100/d2ba885b84032d234a9f9f87ad65ae1f.png) kann als die Menge {0,1,t,t + 1} beschrieben werden (dabei ist t eine Nullstelle von f in
kann als die Menge {0,1,t,t + 1} beschrieben werden (dabei ist t eine Nullstelle von f in 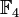 ). Die Rechenregeln ergeben sich aus 1 + 1 = 0 und t2 + t + 1 = 0, beispielsweise
). Die Rechenregeln ergeben sich aus 1 + 1 = 0 und t2 + t + 1 = 0, beispielsweise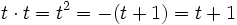
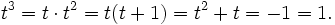
- Aus t(t + 1) = 1 folgt auch t − 1 = t + 1.
Man beachte, dass der Körper
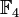 nichts mit dem Restklassenring
nichts mit dem Restklassenring 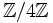 zu tun hat, in dem z. B.
zu tun hat, in dem z. B. 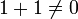 ist und der den Nullteiler 2 enthält (
ist und der den Nullteiler 2 enthält (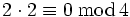 ).
).Der nächstgrößere Oberkörper von
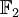 ist
ist 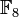 , der z. B. vom Polynom T3 + T + 1 erzeugt wird, also
, der z. B. vom Polynom T3 + T + 1 erzeugt wird, also ![\mathbb F_8\cong\mathbb F_2[T]/(T^3+T+1).](/pictures/dewiki/48/0f14dc965c620c2b2ced100a711b8ad4.png)
Seine Elemente sind
- {0,1,t,t + 1,t2,t2 + 1,t2 + t,t2 + t + 1}
mit t3 = t + 1. Dieser Körper ist aber kein Oberkörper von
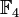 , weil seine Elementanzahl keine Potenz von 4 ist.
, weil seine Elementanzahl keine Potenz von 4 ist.Charakteristik 3
Der Restklassenkörper modulo 3
hat diese Verknüpfungstabellen:
Addition: + 0 1 2 0 0 1 2 1 1 2 0 2 2 0 1 Multiplikation: * 0 1 2 0 0 0 0 1 0 1 2 2 0 2 1 Die ersten Oberkörper von
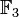 können so dargestellt werden:
können so dargestellt werden:Gegenbeispiel
Die Wahl p = 4 ergäbe folgenden Ring:
Addition: + 0 1 2 3 0 0 1 2 3 1 1 2 3 0 2 2 3 0 1 3 3 0 1 2 Multiplikation: * 0 1 2 3 0 0 0 0 0 1 0 1 2 3 2 0 2 0 2 3 0 3 2 1 Dabei handelt es sich aber nicht um einen Körper. In der Spalte & Zeile für das Element „2“ kommt in der Multiplikationstabelle nirgendwo das neutrale Element vor, folglich hat „2“ kein inverses Element. Das liegt daran, dass in diesem Falle „2“ ein Primfaktor von p = 4 ist. Ein solches Element kommt notwendigerweise in jedem Restklassenring
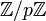 vor, wenn p eine natürliche, nicht-prime Zahl bezeichnet.
vor, wenn p eine natürliche, nicht-prime Zahl bezeichnet.Multiplikative Gruppe
Die multiplikative Gruppe
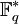 des endlichen Körpers
des endlichen Körpers 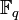 besteht aus allen Elementen des Körpers mit Ausnahme der Null. Die Gruppenoperation ist die Multiplikation des Körpers.
besteht aus allen Elementen des Körpers mit Ausnahme der Null. Die Gruppenoperation ist die Multiplikation des Körpers.Die multiplikative Gruppe ist eine zyklische Gruppe mit q − 1 Elementen. Da deshalb für alle Elemente x dieser Gruppe xq − 1 = 1 gilt, ist jedes Element eine (q − 1)-te Einheitswurzel des Körpers. Diejenigen Einheitswurzeln, die Erzeuger der multiplikativen Gruppe sind, werden als primitive Einheitswurzeln oder Primitivwurzeln bezeichnet. Es sind dies die
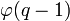 verschiedenen Nullstellen des (q − 1)-ten Kreisteilungspolynoms. (
verschiedenen Nullstellen des (q − 1)-ten Kreisteilungspolynoms. ( bezeichnet die Eulersche φ-Funktion.)
bezeichnet die Eulersche φ-Funktion.)Eigenschaften
Sei p eine Primzahl und q = pn mit
 .
.- Aus xq − 1 = 1 für alle
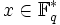 folgt:
folgt:
-
- xq = x für alle
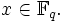
- xq = x für alle
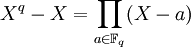 für eine Unbekannte
für eine Unbekannte 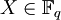
- Zu jedem Teiler k von m gibt es genau einen Zwischenkörper von
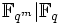 , der isomorph zu
, der isomorph zu 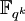 ist. Man könnte auch sagen, dass der Verband der Zwischenkörper von
ist. Man könnte auch sagen, dass der Verband der Zwischenkörper von 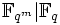 isomorph zum Teilerverband von m ist.
isomorph zum Teilerverband von m ist.
- Ist nämlich K ein Teilkörper von
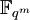 , so ist K ein
, so ist K ein 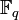 -Vektorraum, also ist die Anzahl der Elemente von K eine Potenz von q. Andererseits ist
-Vektorraum, also ist die Anzahl der Elemente von K eine Potenz von q. Andererseits ist 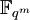 ein Vektorraum über K, und es folgt | K | = qk mit k teilt m. K ist also isomorph zu
ein Vektorraum über K, und es folgt | K | = qk mit k teilt m. K ist also isomorph zu 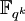 .
. - Ist umgekehrt k ein Teiler von m, so ist das Polynom
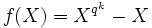 Teiler des Polynoms
Teiler des Polynoms 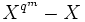 , dessen Nullstellen alle verschieden sind. Deshalb hat f(X) genau qk verschiedene Nullstellen in
, dessen Nullstellen alle verschieden sind. Deshalb hat f(X) genau qk verschiedene Nullstellen in 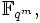 und die Menge der Nullstellen bildet einen Zwischenkörper von
und die Menge der Nullstellen bildet einen Zwischenkörper von 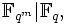 der isomorph zu
der isomorph zu 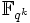 ist.
ist.
- Ist nämlich K ein Teilkörper von
- Die Abbildung
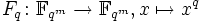 ist ein bijektiver Körperhomomorphismus, sie wird Frobenius-Automorphismus oder einfach Frobenius genannt. Der Fixkörper von Fq ist isomorph zu
ist ein bijektiver Körperhomomorphismus, sie wird Frobenius-Automorphismus oder einfach Frobenius genannt. Der Fixkörper von Fq ist isomorph zu 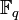 . Die m-fache Verkettung
. Die m-fache Verkettung 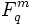 ist die Identität auf
ist die Identität auf 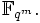
- Da jede endliche Erweiterung von
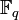 höchstens einen Körper enthält, der isomorph zu
höchstens einen Körper enthält, der isomorph zu 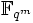 ist, sind Erweiterungen endlicher Körper stets normal.
ist, sind Erweiterungen endlicher Körper stets normal. 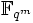 ist der Zerfällungskörper des separablen Polynoms
ist der Zerfällungskörper des separablen Polynoms 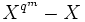 über
über 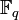 , also sind Erweiterungen endlicher Körper auch stets separabel; endliche Körper sind also vollkommen.
, also sind Erweiterungen endlicher Körper auch stets separabel; endliche Körper sind also vollkommen.- Die Galoisgruppe
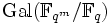 ist zyklisch und hat die Ordnung m. Sie hat einen kanonischen Erzeuger, den Frobenius-Automorphismus Fq.
ist zyklisch und hat die Ordnung m. Sie hat einen kanonischen Erzeuger, den Frobenius-Automorphismus Fq. - Kein endlicher Körper ist algebraisch abgeschlossen: Das Polynom
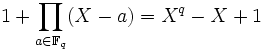 hat keine Nullstelle im Körper
hat keine Nullstelle im Körper 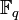 .
.
Anwendungen
Wenn wir einen Erzeuger x der multiplikativen Gruppe von
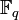 mit q = pn festhalten, dann gibt es für jedes a ungleich 0 aus K eine eindeutig bestimmte Zahl m aus {0, 1, … q-2} mit a = xm. Die Zahl m heißt diskreter Logarithmus von a zur Basis x. Obwohl man xm für jedes m relativ leicht berechnen kann, ist die Aufgabe, zu gegebenem a den diskreten Logarithmus m zu finden, nach dem gegenwärtigen Wissensstand für große Zahlen p und n ein extrem rechenaufwendiger Vorgang. Deshalb findet der diskrete Logarithmus Anwendung in der Kryptographie.
mit q = pn festhalten, dann gibt es für jedes a ungleich 0 aus K eine eindeutig bestimmte Zahl m aus {0, 1, … q-2} mit a = xm. Die Zahl m heißt diskreter Logarithmus von a zur Basis x. Obwohl man xm für jedes m relativ leicht berechnen kann, ist die Aufgabe, zu gegebenem a den diskreten Logarithmus m zu finden, nach dem gegenwärtigen Wissensstand für große Zahlen p und n ein extrem rechenaufwendiger Vorgang. Deshalb findet der diskrete Logarithmus Anwendung in der Kryptographie.Endliche Körper werden auch in der Codierungstheorie benutzt: Viele Codes sind Teilräume von endlichdimensionalen Vektorräumen über endlichen Körpern. Einfachstes Beispiel ist die Verwendung der beiden Elemente 0 und 1 aus
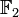 als Codesymbole für binäre Codes.
als Codesymbole für binäre Codes.Literatur
- Dieter Jungnickel: Finite fields: Structure and arithmetics. B.I. Wissenschaftsverlag, 1993, ISBN 3-411-16111-6
- Hans Kurzweil: Endliche Körper. Verstehen, Rechnen, Anwenden. Springer, ISBN 978-3-540-795971
Wikimedia Foundation.

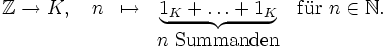
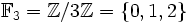
![\mathbb F_9\cong\mathbb F_3[T]/(T^2+1)](/pictures/dewiki/57/972c550611289e4c0369d10ae9e08cd9.png)
![\mathbb F_{27}\cong\mathbb F_3[T]/(T^3-T+1)](/pictures/dewiki/99/c9df942d4e495843d9dab298490c231b.png)