- Hensel lifting
-
Das henselsche Lemma (nach Kurt Hensel) ist eine Aussage aus dem mathematischen Teilgebiet der Algebra.
Inhaltsverzeichnis
Formulierung
Es sei K ein vollständiger, nicht-archimedisch bewerteter Körper mit Bewertungsring A und Restklassenkörper k. Ist nun
![f\in A[X]](/pictures/dewiki/99/c96ad669bd3df95b9703f088ef19bad6.png) ein Polynom, dessen Reduktion
ein Polynom, dessen Reduktion ![\bar f\in k[X]](/pictures/dewiki/99/c7664d19a39dcf09c07472472749c6e7.png) das Produkt zweier teilerfremder Polynome
das Produkt zweier teilerfremder Polynome ![\bar g,\bar h\in k[X]](/pictures/dewiki/101/e62b0f5e13f71f3904d59c7454ea399e.png) ist, so gibt es Polynome
ist, so gibt es Polynome ![g,h\in A[X]](/pictures/dewiki/56/8c41b520cf133d947857bc0732d92a3e.png) , so dass f = gh gilt und
, so dass f = gh gilt und 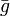 bzw.
bzw.  die Reduktion von g bzw. h ist.
die Reduktion von g bzw. h ist.Beispiele
- Das henselsche Lemma kann dazu benutzt werden, um zu zeigen, dass der Körper der p-adischen Zahlen die (p − 1)-ten Einheitswurzeln enthält:
- Es sei
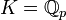 der Körper der p-adischen Zahlen für eine Primzahl p,
der Körper der p-adischen Zahlen für eine Primzahl p, 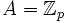 ,
, 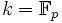 . Das Polynom f(X) = Xp − 1 − 1 zerfällt über k in Linearfaktoren
. Das Polynom f(X) = Xp − 1 − 1 zerfällt über k in Linearfaktoren
- also gibt es Polynome
![g_1,\ldots,g_{p-1}\in\mathbb Z_p[X]](/pictures/dewiki/50/27ac330c12333c1d3e64344ec9d4b73f.png) , so dass
, so dass
- gilt. Die Polynome gi haben notwendigerweise die Form g(X) = aX + b mit
 , man kann also a = 1 annehmen, d.h. es gibt
, man kann also a = 1 annehmen, d.h. es gibt 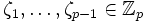 , so dass
, so dass
- gilt, d.h.
 sind die (p − 1)-ten Einheitswurzeln.
sind die (p − 1)-ten Einheitswurzeln.
- Es seien K,A,k wie oben, aber f(X) = Xp − 1. Dann ist
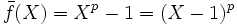 , es gibt also keine Zerlegung von
, es gibt also keine Zerlegung von 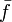 in teilerfremde Faktoren, das henselsche Lemma ist also nicht anwendbar.
in teilerfremde Faktoren, das henselsche Lemma ist also nicht anwendbar.
Verwandte Begriffe
Die Voraussetzung, dass K vollständig ist, ist eigentlich zu stark. Allgemein nennt man bewertete Körper K bzw. Ringe A, in denen das henselsche Lemma in der oben angegebenen Form gilt, henselsch.
Literatur
- Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin 1992, ISBN 3-540-54273-6
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, MR1322960, ISBN 978-0-387-94268-1; 978-0-387-94269-8 .
- Atilla Pethö; Michael Pohst (Hrsg.): Algebraische Algorithmen. Vieweg, 1999, ISBN 9783528065980, S. 187.
- Michael Kaplan: Computeralgebra. Springer, 2005, ISBN 3540213791, S. 51.
- K. Hensel: Theorie der Algebraischen Zahlen. Teubner, Leipzig 1908.
Wikimedia Foundation.

![\bar f(X)=X^{p-1}-1=(X-1)(X-2)\cdots(X-(p-1)),\quad(\mathrm{in}\ \mathbb F_p[X])](/pictures/dewiki/101/effb27440eb9670423c610d9529b8151.png)

![X^{p-1}-1=(X-\zeta_1)\cdots(X-\zeta_{p-1})\quad(\mathrm{in}\ \mathbb Z_p[X])](/pictures/dewiki/51/32ec0d1eb6262fa1ea7a13e2da71ccf2.png)