Hirschman-Index

Der Herfindahl-Index (nach Orris C. Herfindahl) auch Hirschman-Index oder Herfindahl-Hirschman-Index genannt (Abkürzung HHI) ist die am häufigsten benutzte Kennzahl zur Konzentrationsmessung.

Bei der Errechnung des Herfindahl-Index wird von einer Verteilung von Objekten auf mehrere Gruppen ausgegangen: So teilt sich etwa der gesamte Absatz eines Erzeugnisses auf einem bestimmten Markt auf eine bestimmte Anzahl N von Produzenten auf, die das Erzeugnis herstellen. Allerdings verteilt sich der Absatz meist nicht gleichmäßig auf alle Erzeuger. Über das Ausmaß der Konzentration des Absatzes auf einen oder wenige Anbieter gibt nun der Herfindahl-Index H Auskunft, der sich wie folgt errechnet:

$H := \frac{\sum^N_{i=1}{a_i^2}}{(\sum^N_{i=1}{a_i})^2} = \sum^N_{i=1}{\left(\frac{a_i}{N \cdot \overline{a}}\right)^2}$

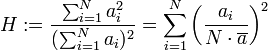
Dabei bedeutet $a_i (i \in [1; N])$ den auf Erzeuger i entfallenden Absatz.

Der Herfindahl-Index ist also die Summe der quadrierten Anteilswerte und kann Werte von 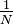$\tfrac{1}{N}$ bis 1 annehmen, wobei der minimale Wert bei Gleichverteilung des Absatzes über alle Anbieter (= minimale Konzentration), der maximale Wert hingegen bei maximaler Konzentration (also wenn der gesamte Absatz auf einen einzigen Anbieter entfällt) erreicht wird. Bei H < 0,10 geht man von einer geringen und bei H > 0,18 bereits von einer hohen Konzentration aus.

Der Herfindahl-Index ist nicht invariant gegenüber der Zahl N der Anbieter. Wird Invarianz gegenüber der Zahl der Anbieter benötigt, dann bieten sich als Alternative andere Ungleichverteilungsmaße an.

Angewandt wird der Herfindahl-Index vor allem in folgenden Bereichen:

• In der Volkswirtschaftslehre sowie im Bereich des Kartellrechts zum Nachweis der marktbeherrschenden Stellung eines oder mehrerer Anbieter: Hohe Werte von H legen nahe, dass einer oder einige wenige Hersteller weite Teile des Marktes kontrollieren, während H = 1 für ein Monopol steht.
• In der Marktforschung als Maßzahl für die Markentreue eines Kunden oder einer Gruppe von Kunden: Je höher H liegt, desto stärker konzentriert sich der Kunde bei seinen Einkäufen auf eine oder wenige Marken. Wird immer die gleiche Marke gekauft, ist H gleich 1.
• In der Betriebssystem-Lehre wenn es um die faire Verteilung von Betriebsmitteln geht.

Siehe auch

• Konzentrationsrate
• Gini-Koeffizient
• Lerner-Index

Literatur

• Bleymüller, Josef / Gehlert, Günther / Gülicher, Herbert: Statistik für Wirtschaftswissenschaftler. WiSt-Studienkurs. München: Vahlen, ¹⁰1996. ISBN 3-8006-2081-2. Kapitel 26.