Homöoid

3-D-Homöoid

2-D-Homöoid

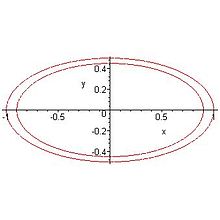
Ein Homöoid ist in drei Dimensionen eine Schale, die durch zwei konzentrische, ähnliche Ellipsoide berandet ist. In zwei Dimensionen ist ein Homöoid ein elliptischer Ring, der durch entsprechende Ellipsen berandet ist.

Mathematische Definition

Wird die äußere Berandung durch ein implizit gegebenes Ellipsoid

$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

mit den Halbachsen $\!\ a, b, c$ beschrieben, so ist für $0 \leq m \leq 1$ die innere Berandung durch

$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=m^2$

gegeben.

Im Grenzfall von $\!\ m \to 1$ spricht man von dünnen, im anderen Fall von dicken Homöoiden.

Physikalische Bedeutung I

Die physikalische Bedeutung eines Homöoiden in der Potentialtheorie liegt darin, dass innerhalb eines homogen mit Masse bzw. Ladung gefüllten Homöoiden auf eine Probemasse bzw. Ladung keine Kraft ausgeübt wird, das heißt, das entsprechende Potential konstant ist. Dies gilt nicht für andere elliptische Schalen (zum Beispiel: Fokaloide). Das Potential im Äußeren eines dünnen Homöoiden ist auf Ellipsoiden konstant, die konfokal zu diesem Homöoiden liegen. Diese bemerkenswerten Eigenschaften wurden bereits von Isaac Newton bewiesen.

Definition homöoidale Verteilung

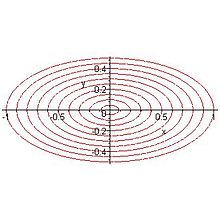
Man spricht von einer homöoidalen Dichteverteilung, wenn die Schichten konstanter Dichte einer Massen- oder Ladungsverteilung durch konzentrische, einander ähnliche Ellipsoide gegeben sind.

Linien konstanter Dichte einer homöoidalen Verteilung

Physikalische Bedeutung II

Innerhalb einer homöoidalen Dichteverteilung tragen zur Kraftwirkung auf einen Körper nur die Schichten bei, die sich innerhalb des zur Berandung konzentrischen, ähnlichen Ellipsoiden befinden, der durch den Körper verläuft.

Literatur

• Subrahmanyan Chandrasekhar: Ellipsoidal Figures of Equilibrium. Yale University Press. London 1969.
• Edward John Routh: A Treatise on Analytical Statics. Vol II. Cambridge University Press, Cambridge 1882.