- Hundsche Kopplungsfälle
-
Die Hundschen Kopplungsfälle stellen die verschiedenen Möglichkeiten der Kopplung von Bahn- und Spin-Drehimpulsvektoren innerhalb eines Moleküls dar. Aufgestellt wurden diese von dem Physiker Friedrich Hund und sind seitdem Teil der quantenmechanischen Beschreibung von Molekülen. Bedeutend sind sie u.a. für die Molekülspektroskopie.
Es werden fünf Fälle unterschieden, die die Hundschen Kopplungsfälle a) bis e) genannt werden, wobei vor allem die Fälle a) und b) von Relevanz sind.
Allgemeines
Ein wichtiger Unterschied zu Atomen ist bei Molekülen, dass sie Schwingungen und Rotationen ausüben können, die Einfluss auf den energetischen Zustand des Moleküls haben. Der Gesamtdrehimpuls
 eines Moleküls setzt sich aus dem Moleküldrehimpuls
eines Moleküls setzt sich aus dem Moleküldrehimpuls  der Kerne sowie den Bahn- und Spin-Drehimpulsvektoren der Elektronen
der Kerne sowie den Bahn- und Spin-Drehimpulsvektoren der Elektronen  und
und  zusammen. Bei der Zusammensetzung wird zwischen verschiedenen Hundschen Kopplungsfällen unterschieden.
zusammen. Bei der Zusammensetzung wird zwischen verschiedenen Hundschen Kopplungsfällen unterschieden.Der Hundsche Kopplungsfall a)
Der Hundsche Kopplungsfall a) tritt bei kleiner Wechselwirkung zwischen der Molekülrotation und der Elektronenbewegung auf. Die Bahn- und Spin-Drehimpulsvektoren
 und
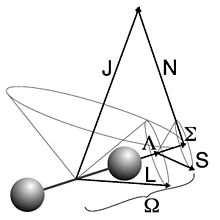
und  der Elektronen sind deshalb an die Molekülachse gebunden, um welche sie in schneller Präzession rotieren. Die Summe ihrer Projektionen auf die Molekülachse (Λ und Σ) wird der totale Elektronen-Drehimpuls Ω genannt. Der Gesamtdrehimpuls
der Elektronen sind deshalb an die Molekülachse gebunden, um welche sie in schneller Präzession rotieren. Die Summe ihrer Projektionen auf die Molekülachse (Λ und Σ) wird der totale Elektronen-Drehimpuls Ω genannt. Der Gesamtdrehimpuls  ist dagegen sowohl von dem Betrag als auch der Richtung her zeitlich konstant.
ist dagegen sowohl von dem Betrag als auch der Richtung her zeitlich konstant.Der Hundsche Kopplungsfall b)
Im Hundschen Kopplungsfall b) ist der Spin-Drehimpulsvektor
 nur schwach oder überhaupt nicht an die Molekülachse gebunden. Die Vektoren Λ und
nur schwach oder überhaupt nicht an die Molekülachse gebunden. Die Vektoren Λ und  addieren sich zu einem Vektor
addieren sich zu einem Vektor  , um den die Molekülachse während der Rotation eine Präzession ausführt. In einer genaueren Beschreibung wird zu
, um den die Molekülachse während der Rotation eine Präzession ausführt. In einer genaueren Beschreibung wird zu  der Spin-Drehimpulsvektor
der Spin-Drehimpulsvektor  der Elektronen hinzu addiert. Das Ergebnis ist der Gesamtdrehimpulsvektor
der Elektronen hinzu addiert. Das Ergebnis ist der Gesamtdrehimpulsvektor  , der wie im Kopplungsfall a) zeitlich konstant ist. Das Molekül führt deshalb eine komplizierte Kreiselbewegung bestehend aus zwei Präzessionen aus.
, der wie im Kopplungsfall a) zeitlich konstant ist. Das Molekül führt deshalb eine komplizierte Kreiselbewegung bestehend aus zwei Präzessionen aus.
Wikimedia Foundation.