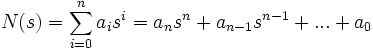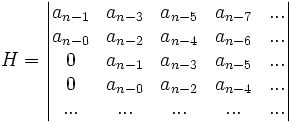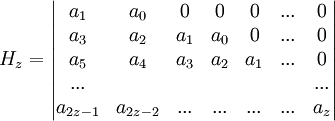Hurwitz-Matrix

Ein Hurwitzpolynom (nach Adolf Hurwitz) ist ein Polynom, dessen Nullstellen einen echt negativen Realteil haben.

Notwendige Bedingung für ein Hurwitzpolynom

Für das Polynom

$N(s) = \sum_{i=0}^n a_i s^i = a_n s^n + a_{n-1} s^{n-1} + ... + a_0$

muss also gelten:

$N(r_i) = 0 \Rightarrow Re\{r_i\} < 0,\quad i=1,\ldots,n.$

Sind die Koeffizienten eines normierten Hurwitzpolynoms (a_n = 1) rein reell, so sind diese auch positiv. Im Umkehrschluss muss ein normiertes Polynom mit rein reellen Koeffizienten, bei dem ein Koeffizient kleiner oder gleich Null ist, eine Nullstelle haben, die keinen echt negativen Realteil besitzt. Das Polynom ist somit kein Hurwitzpolynom.

Anders formuliert: Ist das normierte Polynom ein Hurwitzpolynom, müssen dessen Koeffizienten alle reell, von Null verschieden und positiv sein; diese Bedingung ist notwendig. Für den Fall eines Polynoms 1. (n = 1) oder 2. Grades (n = 2) ist diese Bedingung sogar hinreichend.

Für 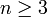$n \ge 3$ (ein Polynom dritten oder höheren Grades) wird eine neue hinreichende und notwendige Bedingung benötigt: die Hurwitz-Determinante.

Hurwitz-Kriterium

Aus den Koeffizienten des Polynoms $a_0 ... a_n\,$ wird zunächst die Determinante der n×n-Hurwitz-Matrix, die sogenannte Hurwitz-Determinante gebildet:

$H=\begin{vmatrix} a_{n-1} & a_{n-3} & a_{n-5} & a_{n-7} & ... \\ a_{n-0} & a_{n-2} & a_{n-4} & a_{n-6} & ... \\ 0 & a_{n-1} & a_{n-3} & a_{n-5} & ... \\ 0 & a_{n-0} & a_{n-2} & a_{n-4} & ... \\ ... & ... & ... & ... & ... \\ \end{vmatrix}$

Nicht vorhandene Koeffizienten werden also durch eine Null ausgedrückt. Das Polynom ist genau dann ein Hurwitz-Polynom, wenn alle "nordwestlichen Unterdeterminanten" (auch Hauptminoren genannt) positiv sind. Die Matrix ist dann positiv definit.

Im Beispiel sind die nordwestliche Unterdeterminanten für den Fall n = 3:

$\begin{align} H_1 &= \begin{vmatrix} a_{n-1} \end{vmatrix} &&= \begin{vmatrix} a_{2} \end{vmatrix} &&= a_{2} > 0 \\[2mm] H_2 &= \begin{vmatrix} a_{n-1} & a_{n-3} \\ a_{n-0} & a_{n-2} \\ \end{vmatrix} &&= \begin{vmatrix} a_{2} & a_{0} \\ a_{3} & a_{1} \\ \end{vmatrix} &&= a_2 a_1 - a_0 a_3 > 0\\[2mm] H_3 &= \begin{vmatrix} a_{n-1} & a_{n-3} & a_{n-5} \\ a_{n-0} & a_{n-2} & a_{n-4} \\ 0 & a_{n-1} & a_{n-3} \\ \end{vmatrix} &&= \begin{vmatrix} a_{2} & a_{0} & 0 \\ a_{3} & a_{1} & 0 \\ 0 & a_{2} & a_{0} \\ \end{vmatrix} &&= a_0 H_2 - a_2 (a_2\cdot 0 - a_3 \cdot 0 ) = a_0 H_2 > 0 \end{align}$ (Entwicklung nach 3. Zeile, 3. Spalte)

Mit unseren Vorüberlegungen zur notwendigen Bedingung ergibt sich also für n = 3 die zusätzliche Forderung a₂a₁ > a₀a₃. Diese ist für a₀ = a₁ = a₂ = a₃ = 1 nicht erfüllt.

Diese Vorgehen ("Verschieben" und "Auffüllen") wird so lange wiederholt, bis eine quadratische (n,n)-Matrix entstanden ist.

In der Literatur finden sich auch andere Definitionen der Hurwitzmatrix. Die Koeffizienten sind oft anders benannt. Hurwitz selber hat in seiner Veröffentlichung das Polynom mit a₀xⁿ + a₁x^{n − 1} + ... + a_n angesetzt.

Eine andere Schreibweise für die Hurwitzdeterminante ist:

$H_{z}=\begin{vmatrix} a_{1} & a_{0} & 0 & 0 & 0 & ... & 0\\ a_{3} & a_{2} & a_{1} & a_{0} & 0 & ... & 0 \\ a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & ... & 0 \\ ... & & & & & & ... \\ a_{2z-1} & a_{2z-2} & ... & ... & ... & ... & a_{z} \\ \end{vmatrix}$

Anwendung

Hurwitzpolynome werden in der Systemtheorie verwendet, um ein System auf asymptotische Stabilität hin zu untersuchen: Ist der Nenner der Systemfunktion ein Hurwitzpolynom, so ist das System asymptotisch stabil.

• Siehe auch: Wurzelsatz von Vieta

Literatur

• Adolf Hurwitz: Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Teilen besitzt. In: Mathematische Annalen Nr. 46, Leipzig 1895, S. 273–285

Weblinks

• Webseite der ETH "Hurwitz Memorial Lecture Series"