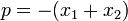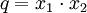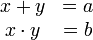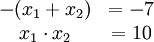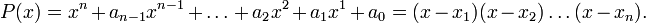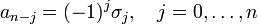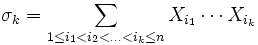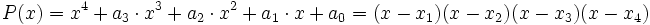- Wurzelsatz von Vieta
-
Der Satz von Vieta oder auch Wurzelsatz von Vieta (nach dem latinisierten Namen von François Viète) gehört in das Teilgebiet der Algebra und macht eine Aussage über den Zusammenhang der Koeffizienten p und q der quadratischen Gleichung
- x2 + px + q = 0
und deren Lösungen (Wurzeln) x1 und x2. Er besagt:
Dies ergibt sich direkt durch Ausmultiplizieren der Nullstellenform nach Koeffizientenvergleich:
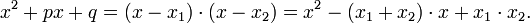
Inhaltsverzeichnis
Beispiele
Für den Satz gibt es drei wichtige Anwendungen:
- 1. Es lassen sich damit quadratische Gleichungen zu vorgegebenen Lösungen konstruieren. Beispielsweise lautet eine quadratische Gleichung zu den Lösungen 2 und 3: x2 − 5x + 6 = 0.
- 2. Es lassen sich Gleichungssysteme der Form
lösen. Z.B. sind die Lösungen x und y des Systems
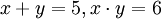 die Lösungen der zugehörigen quadratischen Gleichung z2 − 5z + 6 = 0. Nach der Lösungsformel ergibt sich x=2, y=3 oder x=3, y=2.
die Lösungen der zugehörigen quadratischen Gleichung z2 − 5z + 6 = 0. Nach der Lösungsformel ergibt sich x=2, y=3 oder x=3, y=2.- 3. Der Satz kann helfen die Lösungen bei gegebenen Koeffizienten zu bestimmen (Probiermethode): Ist die quadratische Gleichung
- x2 − 7x + 10 = 0
gegeben, dann muss für die Nullstellen x1, x2 gelten:
Wenn wir zunächst nach ganzzahligen Nullstellen suchen, müssen die Nullstellen Teiler der 10 sein, die zu 7 aufaddiert werden können. Mit etwas Probieren findet man die Nullstellen 2 und 5, da 2+5=7 und
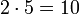 .
.Verallgemeinerung
Der Satz von Vieta über quadratische Gleichungen lässt sich auf Polynomgleichungen bzw. Polynome beliebigen Grades verallgemeinern. Diese Verallgemeinerung des Satzes von Vieta ist die Grundlage für das Lösen von Gleichungen höheren Grades durch Polynomdivision. Nach dem Fundamentalsatz der Algebra gilt:
Jedes (normierte) Polynom n-ten Grades mit Koeffizienten in den komplexen Zahlen lässt sich als Produkt von n Linearfaktoren darstellen:
x1, x2, …, xn sind die Nullstellen des Polynoms; auch wenn alle Koeffizienten a0, a1,… reell sind, können die Nullstellen komplex sein. Nicht alle xi müssen verschieden sein.
Nun ergibt sich der Satz von Vieta durch Ausmultiplizieren und Koeffizientenvergleich:
wobei
die sogenannten Elementarsymmetrischen Polynome in x1 bis xn sind. Für ein Polynom vierten Grades
ergibt sich:
Eine wichtige Anwendung des Satzes für n=2 und n=3 in der Rückführung der kubischen Gleichung auf eine quadratische Gleichung und der Gleichung 4. Grades auf eine kubische Gleichung, der sog. kubischen Resolvente.
Allgemein gilt der Wurzelsatz von Vieta auch für Polynome mit Koeffizienten in anderen Körpern, solange diese nur algebraisch abgeschlossen sind.
Literatur
- Walter Gellert: Lexikon der Mathematik. Leipzig: Bibliographisches Institut, 1990, S.578, 200.
Weblinks
Wikimedia Foundation.