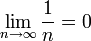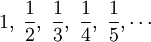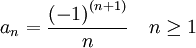Alternierende harmonische Folge
- Alternierende harmonische Folge
-
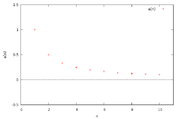
Die ersten 10 Folgeglieder der harmonischen Folge
Die harmonische Folge ist die mathematische Zahlenfolge der Kehrwerte der positiven ganzen Zahlen, also die Folge
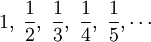 [1]
[1]
mit dem allgemeinen Glied
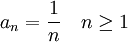 .
.
Jedes Glied der harmonischen Folge mit n ≥ 2 ist das harmonische Mittel seiner Nachbarglieder. Die Summation der Folgenglieder ergibt die harmonische Reihe.
Die alternierende harmonische Folge hat das allgemeine Glied
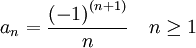 [2]
[2]
Konvergenz
Die harmonische Folge konvergiert gegen Null: 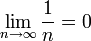
Quellen
- ↑ Uni Heidelberg: Folgen und Reihen Folge (F3) - abgerufen am 13. März 2007
- ↑ Uni Heidelberg: Folgen und Reihen Folge (F7) - abgerufen am 26. Oktober 2006
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Harmonische Folge — Die ersten 10 Folgeglieder der harmonischen Folge Die harmonische Folge ist die mathematische Zahlenfolge der Kehrwerte der positiven ganzen Zahlen, also die Folge … Deutsch Wikipedia
Harmonische Progression — Die ersten 10 Folgeglieder der harmonischen Folge Die harmonische Folge ist die mathematische Zahlenfolge der Kehrwerte der positiven ganzen Zahlen, also die Folge [1] mit dem allgemeinen Glied … Deutsch Wikipedia
Harmonische Zahl — Die harmonische Reihe ist eine spezielle mathematische Reihe. Die harmonische Reihe ist die Folge, deren Glieder die Summen der ersten n Glieder (die Partialsummen) der harmonischen Folge sind. Inhaltsverzeichnis 1 Berechnung 1.1 Werte der ersten … Deutsch Wikipedia
Harmonische Reihe — Die harmonische Reihe ist eine spezielle mathematische Reihe. Die harmonische Reihe ist die Folge, deren Glieder die Summen der ersten n Glieder (die Partialsummen) der harmonischen Folge sind. Inhaltsverzeichnis 1 Berechnung 1.1 Werte der ersten … Deutsch Wikipedia
Alternierende Reihe — Eine alternierende Reihe ist eine Reihe, bei der die Glieder der Folge, welche die Reihe konstruiert, abwechselnd nichtnegativ und nichtpositiv sind: Ein einfaches Beispiel einer alternierenden Reihe ist die alternierende harmonische Reihe im… … Deutsch Wikipedia
Divergente Folge — Eine Folge kann in der Mathematik die Eigenschaft haben, sich mit wachsendem Index immer mehr einer bestimmten Zahl anzunähern. Diese Zahl nennt man Grenzwert oder Limes der Folge. Besitzt eine Folge solch einen Grenzwert, so wird sie konvergent … Deutsch Wikipedia
Konvergente Folge — Eine Folge kann in der Mathematik die Eigenschaft haben, sich mit wachsendem Index immer mehr einer bestimmten Zahl anzunähern. Diese Zahl nennt man Grenzwert oder Limes der Folge. Besitzt eine Folge solch einen Grenzwert, so wird sie konvergent … Deutsch Wikipedia
Grenzwert (Folge) — Eine Folge kann in der Mathematik die Eigenschaft haben, sich mit wachsendem Index immer mehr einer bestimmten Zahl anzunähern. Diese Zahl nennt man Grenzwert oder Limes der Folge. Besitzt eine Folge solch einen Grenzwert, so wird sie konvergent … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
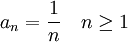 .
.