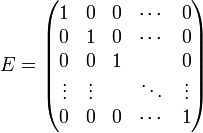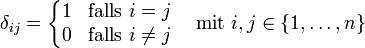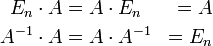Identitätsmatrix

Die Einheitsmatrix oder Identitätsmatrix ist eine quadratische Matrix, deren Hauptdiagonale nur aus Einsen besteht. Alle anderen Elemente sind 0. Die Einheitsmatrix ist die Darstellung der Identitätsabbildung.

Beispiel:

$E = \begin{pmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & & 0 \\ \vdots & \vdots & & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{pmatrix}$

Die Einheitsmatrix ist das neutrale Element unter der Matrizenmultiplikation, d. h. die Multiplikation einer Matrix A mit einer Einheitsmatrix ergibt wieder die Matrix A. Da Matrizen nur miteinander multipliziert werden können, wenn ihre Größen zueinander kompatibel sind, gibt es für jede Größe eine Einheitsmatrix. So ist die Einheitsmatrix der Größe n definiert als Diagonalmatrix mit 1 für alle Elemente der Hauptdiagonale.

Es ist definiert:

$E_1 = \begin{pmatrix} 1 \end{pmatrix} ,\ E_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ,\ E_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ,\ \cdots ,\ E_n = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}$

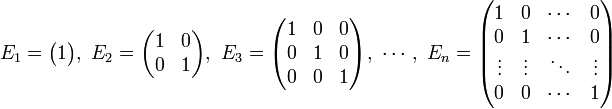
Als Schreibweisen sind E_n (von Einheit) und I_n (von engl. identity) gebräuchlich. Falls aus dem Kontext die Dimension eindeutig hervorgeht, wird auch häufig auf den Index n verzichtet.

Die Komponenten der Einheitsmatrix lassen sich mit dem so genannten Kronecker-Delta

$\delta_{ij} = \left\{\begin{matrix} 1 & \mbox{falls } i=j\\ 0 & \mbox{falls } i \neq j \end{matrix}\right.\quad\mbox{mit }i,j\in\{1,\ldots,n\}$

schreiben. Es ist

$E_n = (\delta_{ij})_{i,j\in\{1,\ldots,n\}}$,

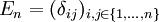oft einfach verkürzt zu

E = (δ_ij)_i,j.

Die Spalten der Einheitsmatrix sind Einheitsvektoren.

Neutrales Element der Allgemeinen Linearen Gruppe

Die invertierbaren Matrizen vom Rang n zusammen mit der Matrizenmultiplikation als Verknüpfung bilden jeweils eine Gruppe, die sogenannte allgemeine lineare Gruppe. Das neutrale Element dieser Gruppe ist die Einheitsmatrix E_n. Für alle Matrizen A dieser Gruppe und ihre Inversen A ^{− 1} gelten die folgenden beiden Rechenregeln.

$\begin{align} E_n \cdot A &= A \cdot E_n &= A\\ A^{-1} \cdot A &= A \cdot A^{-1} &= E_n \end{align}$

Weblinks

• Eric W. Weisstein: Identity Matrix auf MathWorld (englisch)