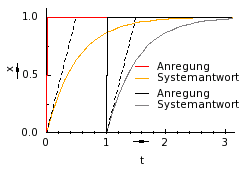
LSI-System

Als ein lineares zeitinvariantes System (LZI System, international LTI linear, time-invariant) wird ein System dann klassifiziert, wenn es zwei Bedingungen erfüllt: Es ist linear und es ist zeitinvariant.

Systemeigenschaften

Damit ein System ein LZI-System ist, müssen die folgenden beiden Eigenschaften gelten: Linearität und Zeitinvarianz.

Linearität bedeutet, dass zwischen Ein- und Ausgangsgröße stets Proportionalität herrscht. Es müssen sowohl das Verstärkungsprinzip als auch das Superpositionsprinzip zutreffen.

Verstärkungsprinzip: Zwei zueinander proportionale Eingangssignale verursachen eine in derselben Weise proportionale Systemantwort.

$x_{a}(t)=T\left[x_{e}(t)\right] \Rightarrow a\cdot x_{a}(t) = T\left[a\cdot x_{e}(t)\right]$

Verstärkungsprinzip

Überlagerungsprinzip, auch Superposition genannt:

Zunächst wird am Eingang des Systems ein Signal angelegt und die Reaktion beobachtet. Danach wird die Reaktion auf ein zweites Signal untersucht. Beim Anlegen eines Eingangssignals, das die Summe aus den beiden zuvor begutachteten Signale bildet, lässt sich feststellen, dass die Reaktion am Ausgang der Addition der beiden einzelnen Antworten entspricht, wenn das System linear ist.

$\lbrace x_{a.a}(t)=T\left[x_{e.a}(t)\right]\wedge x_{a.b}(t)=T\left[x_{e.b}(t)\right] \rbrace \Rightarrow \lbrace x_{a.a}(t)+x_{a.b}(t)=T\left[x_{e.a}(t)+x_{e.b}(t)\right] \rbrace$

Überlagerungsprinzip

Die mathematische Beschreibung eines LZI Systems kann u. a. im Zeitbereich in Zustandsraumdarstellung, also mit einem linearen Differentialgleichungssystem erfolgen.

Für Zeitinvarianz muss die Systemantwort den Zeitbezug zum Eingang beibehalten und identisch reagieren (Verschiebungsprinzip):

$x_{a}(t)=T\left[x_{e}(t)\right] \Rightarrow x_{a}(t+t_{0})=T\left[x_{e}(t+t_{0})\right]$

Verschiebungsprinzip

Demzufolge sind für ein LZI-System die Koeffizientenmatrizen konstant über der Zeit, worauf sich die Bezeichnung zeitinvariant bezieht.

Ein LZI-System kann dynamisches Verhalten aufweisen. Dynamisches Verhalten zeichnet sich dadurch aus, dass der Ausgang nicht nur aktuell zur Veränderung der Eingangsgröße (stationär) reagiert, sondern verzögert über den folgenden Zeitraum hinweg. Hierbei spricht man auch von Einschwingvorgang, Ausgleich oder Verzögerung.

Zunächst wurden nur Eingrößensysteme betrachtet. Mehrgrößensysteme sind komplexer, im einfachsten Fall lassen sie sich so umformen, dass sie in mehrere Eingrößensysteme zerfallen, die sich überlagern. Diese müssen selbstverständlich auch LZI-Eigenschaften aufweisen.

$G(X_a) = G(X_{e.1},X_{e.2}) \Leftrightarrow G(X_a)= G(X_{e.1}) + G(X_{e.2})$

Genauere Betrachtungen erlaubt noch die Zustandsraumdarstellung.

Für einfache Systeme errechnet sich aus dem Faltprodukt von Eingangsfunktion und Impulsantwort die Reaktion am Ausgang.

$x_{a}(t)=g(t)\star x_{e}(t)=\int_{0}^{t}{ g(\tau)\cdot x_{e}(t-\tau)\cdot \mathrm{d}\tau}$

Lässt sich die Impulsantwort nicht direkt bestimmen, kann sie durch Ableiten der Sprungantwort, oder die zweite Ableitung der Rampenantwort ersetzt werden.

LZI-Systeme in verschiedenen Formen der Darstellung

Auf die verwendeten Darstellungsformen selbst wird in den verlinkten Artikeln detailliert eingegangen.

Zeitbereich

Die gebräuchlichste Systemdarstellung im Zeitbereich, die Zustandsraumdarstellung, hat die allgemeine Form

$\begin{matrix} \dot x(t) = Ax(t) + Bu(t) \\ y(t) = Cx(t) + Du(t)\end{matrix}$

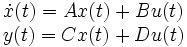
Hierin sind die Vektoren u Eingangsvektor, x Zustandsvektor und y Ausgangsvektor. Sind die Matrizen A Systemmatrix, B Eingangsmatrix, C Ausgangsmatrix und D Durchgriffsmatrix konstant, so ist das System linear und zeitinvariant. Zur Addition und Multiplikation von Vektoren und Matrizen siehe Matrix (Mathematik).

Bildbereich

Für einfachere Systeme, insbesondere SISO-Systeme (Single Input, Single Output Systeme) mit nur je einer Ein- und Ausgangsgröße, wird auch oft noch die Beschreibung durch eine Übertragungsfunktion ("Bildbereich" oder "Frequenzbereich", intern. "frequency domain") gewählt

$H(s) = \frac{Z(s)}{N(s)}$

Hierin ist Z das Zählerpolynom in s, und N das Nennerpolynom in s. Sind alle Koeffizienten beider Polynome konstant, ist das System linear und zeitinvariant.

Die Übertragungsfunktion bietet sich zur graphischen Darstellung als Ortskurve oder Bodediagramm an.

Beispiele

• Elektrotechnik: Filter-Schaltungen oder Verstärker
• Mechanik: Getriebe
• Thermodynamik: Zentralheizung, Motorkühlung
• Wandler zwischen den zuvor genannten Systemarten: Elektromotor (Strom-Kraft), Temperatursensor (Temperatur-Strom)
• Mathematisch (Digitale Simulation): Regler aller Art z. B. PID-Regler

Beispiel aus der Mechanik

Der freie Fall ohne Reibung wird beschrieben durch die Differentialgleichung

$m\ddot z = mg$

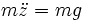
mit dem Weg z, der Beschleunigung an der Erdoberfläche g und der Masse des fallenden Gegenstandes m. Übertragen in die Zustandsraumdarstellung und unter herauskürzen von m erhält man die Zustandsdifferentialgleichung

$\begin{bmatrix} \ddot z \\ \dot z \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \begin{bmatrix}\dot z \\ z \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \end{bmatrix} \begin{bmatrix} g \end{bmatrix}$

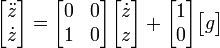
wobei g als (in der Regel konstanter) äußerer Einfluss betrachtet wird, und damit ein (das einzige) Glied des Eingangsvektors bildet. Interessiert man sich naheliegender Weise für die momentane Position p und Geschwindigkeit v, lautet die Ausgangsgleichung

$\begin{bmatrix} v \\ p \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix}\dot z \\ z \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} \begin{bmatrix} g \end{bmatrix}$

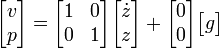
mit einer 1-Matrix als Ausgangsmatrix und einer Nullmatrix als Durchgriffsmatrix, da die Ausgänge identisch mit den Zuständen sind. In dieser Betrachtung handelt es sich um ein LZI System, da alle Matrizen des linearen Differentialgleichungssystems konstant sind.

Berücksichtigt man aber, dass die Erdbeschleunigung g abhängig ist vom Abstand der Massenschwerpunkte

$g = G\,\frac{m_E}{(r_E+z)^2} = G\,\frac{m_E}{r_E^2+2r_Ez+z^2}$

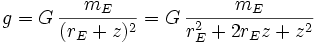
mit der Erdmasse m_E und dem Erdradius r_E, so ist das System nichtlinear abhängig vom Zustand z, also kein LZI System.

Wird die Erdbeschleunigung g aufgrund einer meist sehr viel kleineren Höhe z gegenüber dem Erdradius z < < r_E weiterhin als konstant betrachtet

$g \approx G\,\frac{m_E}{r_E^2}$

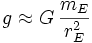
aber die Gleitreibung zwischen betrachteter Masse und Luft als sehr viel einflussreicher in linearer Abhängigkeit von 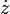$\dot z$ linear berücksichtigt (siehe auch Freier Fall mit Stokes-Reibung), erhält man die Zustandsdifferentialgleichung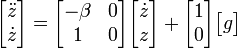

$\begin{bmatrix} \ddot z \\ \dot z \end{bmatrix} = \begin{bmatrix} -\beta &amp;amp;amp; 0 \\ 1 &amp;amp;amp; 0 \end{bmatrix} \begin{bmatrix}\dot z \\ z \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \end{bmatrix} \begin{bmatrix} g \end{bmatrix}$

mit dem Reibkoeffizienten β. Wird β als Formkonstante des fallenden Gegenstandes betrachtet, handelt es sich nach wie vor um ein LZI System.

Literatur

• Heinz Unbehauen: Regelungstechnik 1, Vieweg, Braunschweig/Wiesbaden, ISBN 3-528-93332-1
• Alan V. Oppenheim, Roland W. Schafer, John R. Buck: Zeitdiskrete Signalverarbeitung, Pearson/München, ISBN 3-8273-7077-9