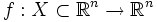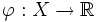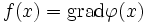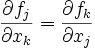Integrabilitätsbedingung — Integrabilitätsbedingung, Mathematik: integrierender Faktor … Universal-Lexikon
Integrabilitätsbedingung — integruotinumo sąlyga statusas T sritis fizika atitikmenys: angl. condition of integrability vok. Integrabilitätsbedingung, f; Integrationsbedingung, f rus. условие интегрируемости, n pranc. condition d’intégrabilité, f … Fizikos terminų žodynas
Gradientfeld — Ein Gradientenfeld ist ein Vektorfeld, das der Gradient einer „Stammfunktion“ sein kann. Das Vektorfeld F ist also genau dann ein Gradientenfeld, wenn es ein Skalarfeld G gibt mit . Dann heißt G Potential. Gradientenfelder zeichnen sich durch… … Deutsch Wikipedia
Totales Differential — Das totale Differential (auch vollständiges Differential) ist ein Begriff aus der Differentialrechnung und bezeichnet das Differential einer Funktion, insbesondere bei Funktionen mehrerer Variablen. Zu einer gegebenen differenzierbaren Funktion… … Deutsch Wikipedia
Gradientenfeld — Ein Gradientenfeld ist ein aus einem Skalarfeld durch Differentiation nach dem Ort abgeleitetes Vektorfeld bzw. – kürzer formuliert – der Gradient eines Skalarfelds. Zur besseren Abgrenzung zwischen dem Gradienten als mathematischem Operator und… … Deutsch Wikipedia
Totales Differenzial — Das totale Differential (auch vollständige Differential) ist ein Begriff aus der Differentialrechnung und bezeichnet das Differential einer Funktion, insbesondere bei Funktionen mehrerer Variablen. Zu einer gegebenen Funktion bezeichnet man mit… … Deutsch Wikipedia
Vollständiges Differential — Das totale Differential (auch vollständige Differential) ist ein Begriff aus der Differentialrechnung und bezeichnet das Differential einer Funktion, insbesondere bei Funktionen mehrerer Variablen. Zu einer gegebenen Funktion bezeichnet man mit… … Deutsch Wikipedia
Dissipatives Kraftfeld — In der Physik heißt ein Kraftfeld konservativ, wenn es nur vom Ort abhängig ist und eine der drei folgenden äquivalenten Eigenschaften besitzt: Es gibt ein skalares Feld , mit , wobei der Gradient ist. Die Arbeit entlang eines beliebigen … Deutsch Wikipedia
Konservatives Feld — In der Physik heißt ein Kraftfeld konservativ, wenn es nur vom Ort abhängig ist und eine der drei folgenden äquivalenten Eigenschaften besitzt: Es gibt ein skalares Feld , mit , wobei der Gradient ist. Die Arbeit entlang eines beliebigen … Deutsch Wikipedia
Konservatives Kraftfeld — In der Physik heißt ein Kraftfeld konservativ, wenn es nur vom Ort abhängig ist und eine der drei folgenden äquivalenten Eigenschaften besitzt: Es gibt ein skalares Feld , mit , wobei der Gradient ist. Die Arbeit entlang eines beliebigen … Deutsch Wikipedia
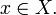
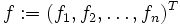 sei auf der offenen und sternförmigen Menge
sei auf der offenen und sternförmigen Menge 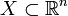 stetig differenzierbar. Unter diesen Voraussetzungen ist f genau dann ein Gradientenfeld, wenn die Integrabilitätsbedingung
stetig differenzierbar. Unter diesen Voraussetzungen ist f genau dann ein Gradientenfeld, wenn die Integrabilitätsbedingung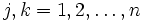 auf X erfüllt ist.
auf X erfüllt ist. , sodass für alle
, sodass für alle  gilt:
gilt: :
: