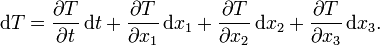- Vollständiges Differential
-
Das totale Differential (auch vollständige Differential) ist ein Begriff aus der Differentialrechnung und bezeichnet das Differential einer Funktion, insbesondere bei Funktionen mehrerer Variablen. Zu einer gegebenen Funktion
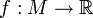 bezeichnet man mit df das totale Differential, z. B.:
bezeichnet man mit df das totale Differential, z. B.:Zur Unterscheidung von totalen und partiellen Differentialen werden hier unterschiedliche Symbole benutzt (nicht-kursives d bzw. kursives d). Hierbei ist M eine offene Teilmenge des reellen Vektorraums
 oder allgemeiner eine differenzierbare Mannigfaltigkeit.
oder allgemeiner eine differenzierbare Mannigfaltigkeit.In den Natur- und Wirtschaftswissenschaften versteht man unter df eine infinitesimale Differenz, in der Mathematik eine Ableitung, die sog. totale Ableitung [df](v) in Richtung des Vektors v,
](/pictures/dewiki/102/f3d884c8c8529f92566eba83a58568f6.png) für
für 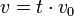 , mit dem zu v gehörenden Einheitsvektor v0. Dabei ist die totale Ableitung von der partiellen zu unterscheiden, weil im letztgenannten Fall nur die explizite Abhängigkeit, bei der totalen Ableitung dagegen auch die impliziten Abhängigkeiten, also mögliche Abhängigkeiten der Parameter mitgezählt werden.
, mit dem zu v gehörenden Einheitsvektor v0. Dabei ist die totale Ableitung von der partiellen zu unterscheiden, weil im letztgenannten Fall nur die explizite Abhängigkeit, bei der totalen Ableitung dagegen auch die impliziten Abhängigkeiten, also mögliche Abhängigkeiten der Parameter mitgezählt werden.Inhaltsverzeichnis
Einfacher Fall
Für eine Funktion f(x,y) von zwei unabhängigen Variablen versteht man unter dem totalen Differential den linearen Differentialausdruck [1]
Dabei bezeichnet
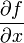 die partielle Ableitung der Funktion f nach der Variablen x. Das totale Differential beschreibt die Änderung von f bei kleinen Änderungen von x und y. Der Begriff kann auf eine beliebige Anzahl von unabhängigen Variablen erweitert werden.
die partielle Ableitung der Funktion f nach der Variablen x. Das totale Differential beschreibt die Änderung von f bei kleinen Änderungen von x und y. Der Begriff kann auf eine beliebige Anzahl von unabhängigen Variablen erweitert werden.Reeller Vektorraum
Für den Fall, dass M der reelle Vektorraum
 ist, erzeugt zu jedem Punkt
ist, erzeugt zu jedem Punkt 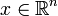 das totale Differential
das totale Differential 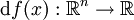 eine lineare Abbildung, die jedem Vektor
eine lineare Abbildung, die jedem Vektor 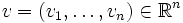 die partielle Ableitung in Richtung dieses Vektors zuordnet, also:
die partielle Ableitung in Richtung dieses Vektors zuordnet, also:Da das totale Differential df(x) als lineare Abbildung interpretiert wird, lässt es sich in folgender Form schreiben
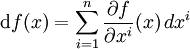 ,
,
wobei
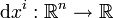 die Linearform ist, die einem Vektor
die Linearform ist, die einem Vektor 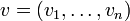 seine i-te Komponente vi zuordnet, d.h.
seine i-te Komponente vi zuordnet, d.h. 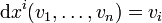 (duale Basis). Unter Zuhilfenahme des Gradienten lässt sich das totale Differential auch wie folgt schreiben:
(duale Basis). Unter Zuhilfenahme des Gradienten lässt sich das totale Differential auch wie folgt schreiben: = \nabla f(x) \cdot v](/pictures/dewiki/49/1075d7dd5dedc485688649996a6bd653.png) ,
,
wobei auf der rechten Seite das Skalarprodukt steht.
Mannigfaltigkeit
Für den allgemeinen Fall ist zu jedem Punkt
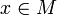 das totale Differential
das totale Differential 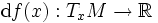 eine lineare Abbildung, die jeder Tangentialrichtung
eine lineare Abbildung, die jeder Tangentialrichtung 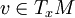 die partielle Ableitung in diese Richtung zuordnet. Ist
die partielle Ableitung in diese Richtung zuordnet. Ist 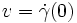 der Tangentialvektor einer Kurve γ in M mit γ(0) = x, so ist
der Tangentialvektor einer Kurve γ in M mit γ(0) = x, so istFür eine Darstellung von df in Koordinaten betrachte man eine Karte
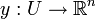 einer Umgebung U des Punkts x mit y(x) = 0. Die n verschiedenen Kurven
einer Umgebung U des Punkts x mit y(x) = 0. Die n verschiedenen Kurven 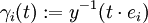 repräsentieren eine Basis
repräsentieren eine Basis 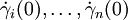 des Tangentialraums TxM und mittels
des Tangentialraums TxM und mittelserhält man die partiellen Ableitungen. Analog zum reellen Vektorraum gilt dann
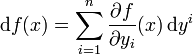 ,
,
wobei
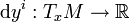 das totale Differential der Funktion
das totale Differential der Funktion 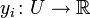 ist. Der Kotangentialraum ist
ist. Der Kotangentialraum ist 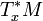 , dual zu den Basisvektoren
, dual zu den Basisvektoren 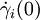 .
.Betrachtet man Tangentialvektoren
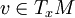 als Derivationen, so gilt [df](x)](v) = v(f).
als Derivationen, so gilt [df](x)](v) = v(f).Integrabilitätsbedingung
Jedes totale Differential A = df ist eine 1-Form, das heißt A besitzt folgende Darstellung
Im Kalkül der Differentialformen wird die Cartan-Ableitung dA als folgende 2-Form beschrieben:
Handelt es sich bei A tatsächlich um ein totales Differential df einer C2-Funktion f, d.h. gilt
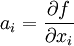 , so ist dA = 0.
, so ist dA = 0.Lokal gilt auch immer die Umkehrung: Erfüllt die 1-Form A die Bedingung dA = 0, so existiert zumindest in einer Umgebung jedes gegebenen Punktes eine Stammfunktion von A, d.h., eine differenzierbare Funktion f, so dass A = df ist.
Man nennt die Bedingung dA = 0 deshalb auch Integrabilitätsbedingung. Ausführlich formuliert lautet sie
- Für alle Indizes i,j gilt
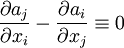 , was im Hinblick auf physikalische Anwendungen auch als verallgemeinerte Rotationsbedingung bezeichnet wird.
, was im Hinblick auf physikalische Anwendungen auch als verallgemeinerte Rotationsbedingung bezeichnet wird.
In vielen Fällen existiert dann sogar eine globale Stammfunktion und A ist tatsächlich ein totales Differential. Das ist zum Beispiel der Fall, wenn der Definitionsbereich der Differentialform A der euklidische Raum
 ist, oder allgemeiner wenn er sternförmig oder einfach zusammenhängend ist.
ist, oder allgemeiner wenn er sternförmig oder einfach zusammenhängend ist.Die Aussage, dass auf einer Mannigfaltigkeit M jede 1-Form, die die Integrabilitätsbedingung erfüllt, eine Stammfunktion besitzt (also ein totales Differential ist), ist äquivalent dazu, dass die erste de-Rham-Kohomologie-Gruppe H1(M) trivial ist.
Hauptsatz der Differential- und Integralrechnung
Betrachtet man
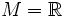 und eine beliebige 1-Form A = fdx. Dann gilt aus Dimensionsgründen immer dA = 0 und die für
und eine beliebige 1-Form A = fdx. Dann gilt aus Dimensionsgründen immer dA = 0 und die für  gültige Integrabilitätsbedingung ist erfüllt. Somit gibt es eine Funktion F, die die Gleichung
gültige Integrabilitätsbedingung ist erfüllt. Somit gibt es eine Funktion F, die die Gleichung 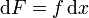 bzw.
bzw. 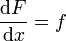 erfüllt. Dies ist gerade der Hauptsatz der Differential- und Integralrechnung für Funktionen einer Variablen.
erfüllt. Dies ist gerade der Hauptsatz der Differential- und Integralrechnung für Funktionen einer Variablen.Verallgemeinerungen
In der Funktionalanalysis kann man den Begriff der totalen Ableitung in naheliegender Weise für Fréchet-Ableitungen verallgemeinern, in der Variationsrechnung für die sog. Variationsableitungen.
Anwendung
Anwendung findet das totale Differential z.B. in der Fluidmechanik. Sei
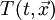 eine Temperatur zum Zeitpunkt t am Ort
eine Temperatur zum Zeitpunkt t am Ort 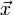 . Interessiert nun die Änderung der Temperatur eines Teilchens zum Zeitpunkt t am Ort
. Interessiert nun die Änderung der Temperatur eines Teilchens zum Zeitpunkt t am Ort 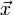 so genügt nicht die Ableitung der Temperatur
so genügt nicht die Ableitung der Temperatur 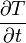 zu betrachten, da das Teilchen nicht nur eine Temperaturänderung sondern auch eine Änderung des Ortes, die sog. konvektive Änderung erfährt. Die Änderung der Temperatur des Teilchen lässt sich nun durch das totale Differential darstellen:
zu betrachten, da das Teilchen nicht nur eine Temperaturänderung sondern auch eine Änderung des Ortes, die sog. konvektive Änderung erfährt. Die Änderung der Temperatur des Teilchen lässt sich nun durch das totale Differential darstellen:Literatur
- Alle Lehrbücher der Analysis, üblicherweise Band 2, „Mehrere Veränderliche“, etc.
Quellen
- ↑ Lothar Papula: Mathematik für Ingenieure. Band 2, 5. Auflage, 1990.
Wikimedia Foundation.

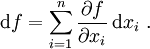
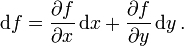
\to\frac{\partial f}{\partial v}(x)=
\frac\operatorname{d}\operatorname{dt}(f(x+t\cdot v))|_{t=0} = \sum_{i=1}^n\frac{\partial f}{\partial x^i}(x)\, v_i](/pictures/dewiki/50/25dff26727a4b42fb2ec74590f4f2e07.png)
 = \frac\operatorname{d}{\operatorname{d}t} \left(f\circ \gamma(t)\right)\Big|_{t=0}\ .](/pictures/dewiki/56/8de9c528c19335a7080ee29cc3eb8f6e.png)
=
\frac\operatorname{d}{\operatorname{d}t}\left(f\circ \gamma_i(t)\right)\Big|_{t=0}](/pictures/dewiki/48/04ba79efd42bc9b275a7509fe3b850e7.png)
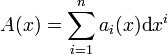
![{\rm d}A(x) = \sum_{i=1}^n\sum_{j=i+1}^n \left[\frac{\partial a_j}{\partial x_i}(x)-\frac{\partial a_i}{\partial x_j}(x)\right] \operatorname{d}x^i\wedge \operatorname{d}x^j](/pictures/dewiki/55/710bbfa8ad40037c40dae016cf6b042d.png)