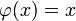Iterationsmatrix

Die Fixpunktiteration ist ein in der Mathematik gebräuchliches iteratives Verfahren zur näherungsweisen Bestimmung der Nullstellen einer Funktion f auf einem bestimmten Intervall [a,b]. Die Gleichung muss dazu zuerst in eine Fixpunktgleichung, also eine Gleichung der Form

$\varphi(x) = x$

umgeformt werden.

Allgemein

Jedes Fixpunktverfahren hat die Form

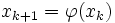$x_{k+1} = \varphi(x_k)$, k = 0, 1, ...

Mit jeder weiteren Iteration soll sich x_k+1 der exakten Lösung x^* annähern. Das Ziel ist, die Iterationsvorschrift $\varphi$ so zu konstruieren, dass sie genau einen Fixpunkt x^* besitzt, dass also schließlich gilt:

$x^* = \varphi(x^*)$.

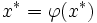Die Konvergenz von Fixpunktiterationen wird mittels des banachschen Fixpunktsatzes untersucht. In vielen Fällen divergiert die Iteration auch, so dass kein Fixpunkt ermittelt werden kann. Die Konvergenz hängt außer von der Funktion insbesondere vom gewählten Startwert der Iteration ab.

Lineare Fixpunktverfahren

Konstruktionsidee

Eine wichtige Art der Fixpunktiteration sind die Splitting-Verfahren. Für Fixpunkt-Probleme der Art Ax = b, wobei A eine nicht-singuläre quadratische Matrix und b ein Vektor ist, zerlegt man die Matrix A mit Hilfe einer nicht-singulären n×n-Matrix B in

A = B + (A − B)

und erhält so eine Fixpunktgleichung.

Damit folgt

Ax = b

(B + (A − B))x = b

Bx + (A − B)x = b

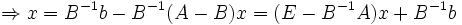$\Rightarrow x = B^{-1}b - B^{-1}(A-B)x = (E - B^{-1}A)x + B^{-1}b$; E ist die Einheitsmatrix.

Jetzt ist das lineare Gleichungssystem Ax = b äquivalent zu der Fixpunktaufgabe

$x = (E - B^{-1}A)x + B^{-1}b = \varphi(x)$.

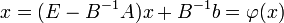Man erhält für den vorgegebenen Startvektor x₀ folgendes Iterationsverfahren

x_{k + 1} = (E − B ^{− 1}A)x_k + B ^{− 1}b, k = 0, 1, ...

und die zugehörige Iterationsmatrix lautet: E - B^-1A.

Konvergenz

Aus dem banachschen Fixpunktsatz und weiteren Überlegungen folgt dann, dass diese Fixpunktverfahren genau dann für jeden Startvektor x₀ konvergieren, falls der Spektralradius der Iterationsmatrix

ρ(E − B ^{− 1}A) = max_i | λ_i(E − B ^{− 1}A) | < 1.

ρ(E − B ^{− 1}A) sollte möglichst klein sein, da dadurch die Konvergenzgeschwindigkeit bestimmt wird.

Spezielle Verfahren

Auf obiger Konstruktionsidee basieren folgende bekannte Verfahren:

• Gauß-Seidel-Verfahren oder auch Einzelschrittverfahren (ESV)
• Jacobi-Verfahren oder auch Gesamtschrittverfahren (GSV)

Bemerkungen

Iterationsverfahren der Form x_{k + 1} = Mx_k + v, k = 0, 1, ... sind

• linear, d.h. x_k+1 hängt linear nur von x_k ab,
• stationär, d.h. M und v sind unabhängig von der Schrittnummer der Iteration,
• einstufig, d.h. nur der letzte und nicht noch weitere Näherungsvektoren werden verwendet.

Nichtlineare Gleichungen

Das Newton-Verfahren kann als Fixpunktiteration betrachtet werden. Allgemein wird die Konvergenz mit Hilfe des banachschen Fixpunktsatzes sichergestellt, die betrachtete Funktion muss also insbesondere im betrachteten Gebiet eine Kontraktion sein.