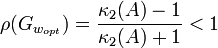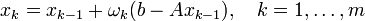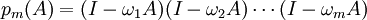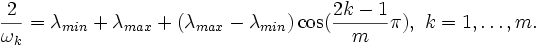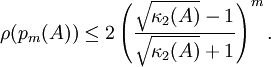Richardson-Iteration

Das Richardson-Verfahren ist in der numerischen Mathematik ein Algorithmus zur näherungsweisen Lösung von linearen Gleichungssystemen. Es zählt wie das Gauß-Seidel-Verfahren zur Klasse der Splitting-Verfahren. Als iteratives Verfahren nähert es sich schrittweise einer Lösung des linearen Gleichungssystems Ax = b an.

Richardson-Verfahren

Durch Wahl von B = I (Einheitsmatrix) erhält man aus der allgemeinen Fixpunktgleichung

x = Φ(x): = Ix − B ^{− 1}Ax + B ^{− 1}b

das Richardsonverfahren.

x_{k + 1} = (I − A)x_k + b

Dieses Verfahren konvergiert wie jede Fixpunktiteration dieser Art, falls der Spektralradius der Iterationsmatrix G: = I − A echt kleiner eins ist.

Relaxiertes Richardsonverfahren

Die Iterationsformel des relaxierten Richardson-Verfahrens lautet

x_{k + 1} = (I − ωA)x_k + ωb

Dabei wird in jedem Schritt das Residuum mit einem Faktor ω gewichtet. Falls A eine symmetrisch positiv definite Matrix ist so gilt für den optimalen Relaxionsparameter

$\omega_{opt} = \frac{2}{\lambda_{max}(A) + \lambda_{min}(A)}$.

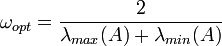Dabei bezeichnen λ_max(A) und λ_min(A) den maximalen und minimalen Eigenwert von A. Für den Konvergenzradius (gleichbedeutend zum Spektralradius) gilt

$\rho(G_{w_{opt}}) = \frac{\kappa_2(A) - 1}{\kappa_2(A) + 1} < 1$

dabei bezeichnet κ₂(A) die Kondition der Matrix A. Das relaxierte Richardson-Verfahren konvergiert dann genauso "schnell" wie das Gradientenverfahren bei symmetrischen Matrizen, wofür man jedoch keinen Relaxionsparameter berechnen muss. Dafür kann man mit dem Richardsonverfahren auch bei unsymmetrischen Matrizen mit komplexen Eigenwerten noch Konvergenz erzwingen, solange deren Realteile alle positiv sind.

Das Verfahren ist als Glätter in Mehrgitterverfahren geeignet.

Zyklisches Richardsonverfahren

Die Konvergenz lässt sich erheblich verbessern, wenn man mehrere Schritte der Iteration mit unterschiedlichen Parametern ω_k betrachtet. Man führt dazu jeweils m Schritte

$x_k = x_{k-1} + \omega_{k}(b-Ax_{k-1}),\quad k=1,\ldots,m$

zyklisch durch. Das Verfahren konvergiert, wenn der Spektralradius des Matrixpolynoms

$p_m(A) =(I-\omega_1 A)(I-\omega_2 A)\cdots (I-\omega_m A)$

kleiner als eins ist, und umso besser je kleiner er ist. Für eine Matrix A mit reellen und positiven Eigenwerten kann der Spektralradius durch das Maximum des reellen Polynoms 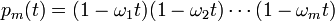$p_m(t) =(1-\omega_1 t)(1-\omega_2 t)\cdots (1-\omega_m t)$ im Intervall [λ_min,λ_max] abgeschätzt werden. Besonders klein wird dieses Maximum, wenn man die Relaxationsparameter so wählt, dass ihre Kehrwerte gerade die Nullstellen des geeignet verschobenen Tschebyschow-Polynoms sind,

$\frac2{\omega_k}=\lambda_{min}+\lambda_{max} +(\lambda_{max}-\lambda_{min})\cos(\frac{2k-1}{m}\pi),\ k=1,\ldots,m.$

Dann verbessert sich die Konvergenzaussage für symmetrische Matrizen und einen Zyklus der Länge m zu

$\rho(p_m(A))\le 2\left(\frac{\sqrt{\kappa_2(A)}-1}{\sqrt{\kappa_2(A)}+1}\right)^m.$

Für realistische Probleme mit 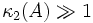$\kappa_2(A)\gg1$ stellt dies eine große Verbesserung gegenüber dem einfachen relaxierten Verfahren dar, da nur noch die Wurzel der Konditionszahl eingeht.

Für symmetrisch-definite Matrizen bietet dieses Verfahren kaum Vorteile gegenüber dem Verfahren der konjugierten Gradienten, da es die Schätzung der Eigenwerte λ_min,λ_max erfordert. Im unsymmetrischen Fall können aber die Parameter auch für komplexe Eigenwerte gut angepasst werden, vgl. Literatur. In den meisten Fällen ist aber die Tschebyschow-Iteration vorzuziehen, da sie die gleiche Fehlerschranke für jeden Iterationsschritt und nicht nur für Vielfache der Zykluslänge 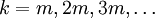$k = m, 2m, 3m, \ldots$ erreicht.

Literatur

• Andreas Meister: Numerik linearer Gleichungssysteme. 2. Auflage. Vieweg 2005, ISBN 3-528-13135-7
• Bernd Fischer, Lothar Reichel: A stable Richardson iteration method for complex linear systems. Numer. Math. 54 (1988), 225-242.