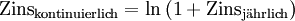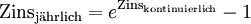Jahreszinsfuß

Abzinsung (Beispielhafte Übersicht)

Der Zinssatz, auch Zinsfuß, ist der in Prozent ausgedrückte Preis für geliehenes Kapital, also der Zins als Prozentangabe.

Nomenklatur

Größensymbole

In der sich mit Zins und Zinssätzen beschäftigenden Literatur findet man sowohl die Bezeichnung i als auch die Bezeichnung r. Da sich mittlerweile jedoch international die Bezeichnung i durchzusetzen scheint, wird diese Bezeichnung hier verwendet.

Unterscheidung von Zinssatz und Zinsfuß

Manchmal wird präzise Zinsfuß und Zinssatz wie folgt unterschieden:

Zinsfuß p = Wert (z. B. 10)

Zinssatz i = p/100 (z. B. 0,1 = 10 %)

Berechnungsmethoden

Allgemeine Zinsformel

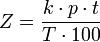$Z = \frac{k \cdot p \cdot t}{T \cdot 100}$ oder: $Z = \frac{k \cdot i \cdot t}{T}$

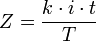
k … Kapital in Geldeinheiten

p … Zinssatz in Prozent

t … Verzinsungszeit in Tagen

T … Tageteiler (Jahresbemessungsgrundlage)

Bemessungsgrundlage des Zinssatzes i

Üblicherweise ist der Zinssatz bezogen auf ein Jahr (p. a., pro anno/per annum). Daneben kommen auch monatliche Zinssätze p. M. pro mese und solche nach Quartal (p. Qu) vor.

Bankjahr: Usancen der Zeiteinheiten t/T

Zur korrekten Verwendung der Zinsformel bezüglich Tage t und Tageteiler T ist immer auch die Angabe der Berechnungsmethode wichtig. Diese Usancen nennt man allgemein das Bankjahr.

Die Berechnungsmethode gibt an, wie bei Laufzeiten unter einem Jahr zu verfahren ist. Es gibt folgende Methoden:

• 30/360 (Deutsche Methode): Das Jahr wird mit 360 Tagen gerechnet, jeder Monat immer mit 30 Tagen
• act/360 (Euromethode od. Französische Usance): Das Jahr wird mit 360 Tagen gerechnet, beim Monat zählen die tatsächlichen Tage (actual, deutsch klm ‚kalendermäßig‘)
• act/365 (Englische Methode): Das Jahr wird als kalendermäßiges Gemeinjahr mit 365 Tagen gerechnet, beim Monat zählen die tatsächlichen Tage (actual)
• act/act (tagegenaue Methode): Sowohl das Jahr als auch der Monat werden mit den tatsächlichen Tagen gerechnet, (actual). Dabei wird die Zinsperiode aufgeteilt, wenn Schaltjahre enthalten sind, und für jeden Teil werden die zugehörigen Teiler verwendet. (Beispiel: 20. Dezember 2007 bis 20. Januar 2008: 31 Tage, aufgeteilt in 11 Tage / 365 und 20 Tage / 366)

An den Geldmärkten im Euroland ist mittlerweile die Methode act/360 üblich.

Im Normalfall wird der erste Tag (der Tag der Aufnahme des Zinsgeschäfts) nicht miteingerechnet.

Als Beispiel diene ein Zinssatz von i = 5% = 0,05 und ein Kapitalbetrag von k = 100.000,00 Euro. Das Geld wird vom 15. Februar 2008 bis 15. März 2008 (ein Schaltjahr) angelegt (Anlageaufnahme also am 14. Februar 2008). Damit ergeben sich folgende Zinszahlungen:

• 30/360: $k \cdot i \frac{30}{360} = 416{,}67$
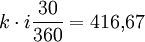
• act/360: $k \cdot i \frac{29}{360} = 402{,}78$
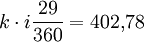
• act/365: $k \cdot i \frac{29}{365} = 397{,}26$
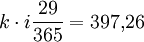
• act/act: $k \cdot i \frac{29}{366} = 396{,}17$

Zinseszins-Effekt: Jährlicher und kontinuierlicher Zinssatz

Den Einfluss des Zinseszins-Effektes auf das Ergebnis zeigt ein einfaches Rechenbeispiel:

Wenn man einen Euro für ein Jahr zu einem Zinssatz von 100 Prozent anlegt und jährlich die Zinsen ausgezahlt bekommt, erhält man nach Ablauf dieses einen Jahres 1 € Guthaben + 1 € Zinsen = 2 €. Bei einer Zinsgutschrift alle 6 Monate werden dagegen nach einem halben Jahr für den ersten Euro 0,5 € Zinsen gutgeschrieben und nach einem weiteren halben Jahr für die ab jetzt insgesamt verzinsten 1,5 € weitere 0,75 €. Am Ende hat man also ein Gesamtergebnis von 1 € Guthaben + 1,25 € Gesamtzinsen = 2,25 €. Bei monatlicher Ausschüttung erhält man nach Ablauf eines Jahres schon 2,61 €. Werden die Zinsen in immer kürzeren Intervallen gutgeschrieben und mitverzinst, so strebt der Auszahlungsbetrag gegen einen Grenzwert von 2,718282 €. Dieser Wert wird Eulersche Zahl e ≈ 2,718282 genannt.

Jedem Zinssatz aus kontinuierlicher Verzinsung entspricht ein Zinssatz in jährlicher Verzinsung (p. a.) nach folgender Formel:

$\mathrm{Zins}_\mathrm{kontinuierlich} = \ln{(1 + \mathrm{Zins}_{\mathrm{j\ddot{a}hrlich}})}$

$\mathrm{Zins}_{\mathrm{j\ddot{a}hrlich}} = e^{\mathrm{Zins}_\mathrm{kontinuierlich}} - 1$

Ein jährlicher Zinssatz von 20 % entspricht also einem kontinuierlichem Zinssatz von 18,23 %.

Für Zeiträume, die von einem Jahr abweichen, ist es oft günstiger, mit Zinssätzen in kontinuierlicher Verzinsung zu rechnen. Stundengenaue Rechnung ist im Bankwesen nicht üblich.

Arten der Zinssätze

Man unterscheidet verschiedene Arten von Zinssätzen, beispielsweise:

• Nominalzinssatz: reiner Zinssatz, mit dem der Zinsbetrag errechnet wird
• Realzinssatz: Bereinigung des Zinssatzes um die Wirkungen der Inflation
• Effektivzinssatz: Einbeziehung von Auszahlungskurs, Nebenkosten und unterperiodigen Zinszahlungen

Grundzinssätze der Gesamtwirtschaft sind Leitzinssatz für Interbankkredite, und Eckzinsatz für Spareinlagen.

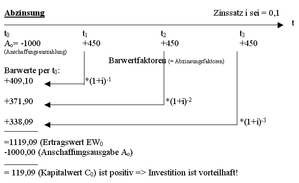
Interner Zinsfuß

Der interne Zinsfuß ist derjenige Zinssatz, bei dem der Kapitalwert einer Zahlungsreihe oder eines Projektes der Definition nach genau Null ist. Hieraus lässt sich mithilfe der Methode des internen Zinsfußes schließen, ob die Durchführung dieses Projektes vorteilhaft ist oder nicht. Vorteilhaft – und daher einen positiven Kapitalwert liefernd – ist das Projekt immer dann, wenn der Kalkulationszinssatz niedriger ist als der interne Zins, unvorteilhaft in dem Falle, wenn der Kalkulationszinssatz höher liegt. Auch als Effektivzins (bei Finanzierungen) oder Internal Rate of Return (IRR) bezeichnet.

Kalkulationszinsfuß

Der Kalkulationszinsfuß oder Kalkulationszinssatz (engl. hurdle rate oder required rate of return) wird in der Investitionsrechnung bei Discounted Cash-Flow Analysen verwendet. Er bezeichnet die subjektive Mindestverzinsungsforderung eines Anlegers an seine Investition und bestimmt, wie stark weiter in der Zukunft liegende Zahlungen auf ihren Barwert abgewertet werden. Der Kalkulationszinsfuß wird ermittelt, indem die Kapitalkosten oder gewichteten Kapitalkosten um eine Risikoprämie erhöht (Investition) oder vermindert (Kreditvergabe) werden.

Unter Berücksichtigung des Zeitwertes des Geldes wird deutlich, dass die Forderung nach einer hohen Rendite gleichbedeutend mit der Forderung nach riskanteren und kurzfristigeren Investitionen ist, da gegenwartsnahe Zahlungen relativ stärker bewertet werden als spätere.

Siehe auch

• Formelsammlung Betriebswirtschaftslehre
• Lieferantenkredit
• Zinsrechnung
• Skonto