Kapitalwert

Der Kapitalwert (englisch: net present value [NPV] = Net-Present-Value oder Nettogegenwartswert [seltener: NGW]; auch: Barwert [aller Zahlungen]) ist eine betriebswirtschaftliche Kennziffer der dynamischen Investitionsrechnung. Durch Abzinsung auf den Beginn der Investition werden Zahlungen, die zu beliebigen Zeitpunkten anfallen, vergleichbar gemacht.

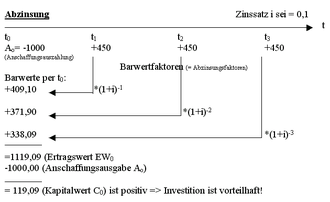
Der Kapitalwert einer Investition ist die Summe der Barwerte aller durch diese Investition verursachten Zahlungen (Ein- und Auszahlungen). Voraussetzung ist jedoch, dass zwischenzeitliche kumulierte Überschüsse sofort zum Kalkulationszinssatz angelegt werden (Wiederanlageprämisse). (Zum besseren Verständnis der Rechenoperation kann der Kapitalwert auch als der errechnete Geldbetrag betrachtet werden, der eingesetzt werden müsste, um nach vorher kalkulierten Abhebungen unter Berücksichtigung der Verzinsung am Ende der Betrachtung zu einem Saldo von 0 zu gelangen.)

Die Kapitalwertmethode oder Barwertmethode (weniger verbreitet: NPV-Methode bzw. Net-Present-Value-Methode oder NGW-Methode)^[1] erlaubt die Beurteilung einer Erweiterungsinvestition und die Bestimmung des Ersatzzeitpunktproblems. Methodologisch entspricht die Kapitalwertmethode der Discounted-Cash-Flow-Methodik, die bei u. a. Unternehmensbewertungen zum Einsatz kommt.

Berechnung

Abzinsung (Beispielhafte Übersicht)

Der Kapitalwert ist abhängig vom Kalkulationszinssatz und basiert auf der Annahme des vollkommenen Kapitalmarktes.

Der Kapitalwert berechnet sich, wie folgt:

• $C_0 = -I+\sum_{t=1}^T \left(R_t\right)\cdot\left( 1+i \right)^{-t} +L\cdot\left( 1+i \right)^{-T}$
• C₀: Kapitalwert
• I: Investition
• T: Betrachtungsdauer (in Perioden)
• R_t: Rückfluss (Cashflow) in Periode t, wobei R_t = EW_t − A_t (Ertragswert − Anschaffungsausgaben) darstellt.
• L: Liquidationserlös/Resterlös
• i: Kalkulationszinssatz

Fallen während der Nutzungsdauer pro Periode stets gleiche Zahlungen an, kann der Kapitalwert auch einfach mithilfe der Rentenbarwertformel ermittelt werden:

• $C_0 = -I + R_T\cdot\frac{\left( 1+i \right)^T - 1}{\left( 1+i \right)^T \cdot i} + L\cdot \left( 1+i \right)^{-T}$
• R_T: Rückfluss pro Periode

Anmerkung: Bei den Liquidationserlösen wird nicht der Buchwert (Abschreibungen) sondern der erwartete Verkaufserlös zur Berechnung herangezogen.

Für unterschiedliche Zinsfaktoren in den verschiedenen Perioden errechnet sich der Kapitalwert, wie folgt:

• $C_0 = -I+\frac{R_1}{q_1}+\frac{R_2}{q_1\cdot q_2}+\frac{R_3}{q_1\cdot q_2\cdot q_3}+\ldots = -I+\sum\limits^{n}_{j=1}\cdot\frac{R_j}{\prod\limits^{j}_{l=1}q_l}$
• R_j: Rückfluss in Periode j
• q_l: Zinsfaktor der Periode l mit q = 1 + i

Interpretation

Eine Investition ist absolut vorteilhaft, wenn ihr Kapitalwert größer als Null ist.

Kapitalwert = 0: Der Investor erhält sein eingesetztes Kapital zurück und eine Verzinsung der ausstehenden Beträge in Höhe des Kalkulationszinssatzes. Die Investition hat keinen Vorteil gegenüber der Anlage am Kapitalmarkt zum gleichen (risikoäquivalenten) Zinssatz. An dieser Stelle befindet sich der interne Zinsfuß.

Kapitalwert > 0: Der Investor erhält sein eingesetztes Kapital zurück und eine Verzinsung der ausstehenden Beträge, die den Kalkulationszinssatz übersteigen.

Kapitalwert < 0: Die Investition kann eine Verzinsung des eingesetzten Kapitals zum Kalkulationszinssatz nicht gewährleisten.

Werden mehrere sich gegenseitig ausschließende Investitionsalternativen verglichen, so ist die mit dem größten Kapitalwert die relativ vorteilhafteste. Weiterhin ist es möglich, die Kapitalwerte verschiedener sich nicht gegenseitig ausschließender Investitionen mit unterschiedlichen Kalkulationszinssätzen aufzusummieren, da es sich um ein additives Verfahren handelt.

Kritik

Vorteile

Es handelt sich um ein rechnerisch einfaches Verfahren, das eine leichte Interpretation ermöglicht, da der Kapitalwert in Geldeinheiten ausgedrückt wird (absolutes Ergebnis). Es ist weiterhin möglich zinsstrukturkonforme Berechnungen durchzuführen, da der Kalkulationszinssatz in jeder Periode angepasst werden kann. Zusätzlich kommen bei der Kapitalwertmethode die Vorteile der dynamischen Rechnung (Beachtung des zeitlichen Anfalls der Zahlungen) gegenüber der statischen Rechnung zum Tragen.

Nachteile

Problematisch beim Einsatz der Kapitalwertmethode, wie auch allen anderen Discounted-Cash-Flow-Verfahren, sind die Annahme des vollkommenen Kapitalmarktes, insbesondere die Annahme der Gleichheit von Soll- und Habenzinssatz, der auf subjektiven Annahmen basierende Kalkulationszinssatz und die Höhe der zukünftigen Zahlungsströme. Aufgrund der einfachen Berechnung und Interpretierbarkeit besteht die Gefahr, die Ergebnisse unkommentiert zu verwenden. Es ist daher wichtig, dass die getroffenen Annahmen, vor allem über die Höhe der Risikoprämie des Kalkulationszinssatzes und der künftigen Cashflows, genannt und begründet werden.

Wird die Möglichkeit, eine Investition mehrmals zu tätigen, übersehen, so kann dies zu Fehlentscheidungen führen. Abhilfe schafft hier die Annuitätenmethode. Hierbei wird von einer Wiederanlage der Erträge zum Kapitalmarktzins ausgegangen.

Siehe auch

• Interner Zinsfuß
• Endwertmethode
• Formelsammlung Betriebswirtschaftslehre

Literatur

• Louis Perridon, Manfred Steiner: Finanzwirtschaft der Unternehmung. 14. überarbeitete und erweiterte Auflage. Franz Vahlen Verlag, München 2007, ISBN 978-3-8006-3359-3, 732 S. (Vahlens Handbücher der Wirtschafts- und Sozialwissenschaften).
• Jean-Paul Thommen: Managementorientierte Betriebswirtschaftslehre. 7. überarbeitete und ergänzte Auflage. Versus Verlag, Zürich 2004, ISBN 3-03909-000-3, 960 S.
• Rudolf Volkart: Corporate Finance. Grundlagen von Finanzierung und Investition. 3. überarbeitete und erweiterte Auflage. Versus Verlag, Zürich 2007, ISBN 978-3-03-909091-4, 1343 S.

Einzelnachweis

1. ↑ Horst Hanusch: Nutzen – Kosten – Analyse. 2. Aufl. Wirtschaftswissenschaftliche Fakultät der Universität Augsburg, 2004. S. 23, 27 ff. (PDF-Datei; 141 kB)