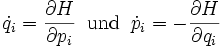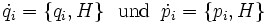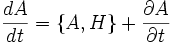Hamiltonsche Bewegungsgleichungen
Schlagen Sie auch in anderen Wörterbüchern nach:
Hamiltonsche Bewegungsgleichung — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Hamiltonsche Gleichungen — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Hamiltonsche Mechanik — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Hamilton-Formalismus — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Hamilton-Gleichung — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Hamiltonformalismus — Die hamiltonsche Mechanik ist ein Teilgebiet der klassischen Mechanik. Sie untersucht die Bewegung im Phasenraum. Dabei handelt es sich um die Menge der Paare von Orts und Impulswerten, die man bei dem betrachteten System von Teilchen anfänglich… … Deutsch Wikipedia
Kanonische Gleichungen — Die kanonischen Gleichungen sind in der klassischen Mechanik die Bewegungsgleichungen eines Systems, das durch eine Hamiltonfunktion H = H(q,p,t) beschrieben wird, und werden deshalb auch Hamiltonsche Bewegungsgleichungen genannt. Sie lauten und … Deutsch Wikipedia
Kanonische Transformation — In der klassischen Mechanik bezeichnet man eine Koordinatentransformation im Phasenraum als kanonisch, wenn sie die Hamiltonschen Gleichungen invariant lässt. Ziel dabei ist, die neue Hamilton Funktion möglichst zu vereinfachen, im Idealfall… … Deutsch Wikipedia
Hamilton'sches Prinzip — Das Hamiltonsche Prinzip oder das Prinzip der kleinsten Wirkung ist ein Extremalprinzip. Danach verhalten sich die physikalischen Teilchen und Felder so, dass eine Größe, die die Teilchenbahnen und Felder bewertet, kleiner ist als bei allen… … Deutsch Wikipedia
Hamilton-Prinzip — Das Hamiltonsche Prinzip oder das Prinzip der kleinsten Wirkung ist ein Extremalprinzip. Danach verhalten sich die physikalischen Teilchen und Felder so, dass eine Größe, die die Teilchenbahnen und Felder bewertet, kleiner ist als bei allen… … Deutsch Wikipedia