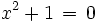- Klassische Algebra
-
Als klassische Algebra bezeichnen wir das Teilgebiet der Mathematik, das sich mit der Auflösung algebraischer Gleichungen beschäftigt.
Der Begriff klassische Algebra ist keineswegs allgemein eingeführt; er wird mitunter verwendet, um eine Abgrenzung von der elementaren (Schul-)algebra einerseits und von der abstrakten (Struktur-orientierten) Algebra andererseits zu ermöglichen. Siehe den Artikel Algebra für Wortgeschichte und grobe Übersicht.
Eine Gleichung heißt algebraisch, wenn zu ihrer Formulierung nur endlich viele elementare Rechenoperationen (Addition, Subtraktion, Multiplikation, Division) erforderlich sind.
Eine algebraische Gleichung erhält man durch Nullsetzen eines Polynoms, also z.B.:
Der Grad des Polynoms ist dann der Grad der Gleichung. Gleichungen 1., 2. beziehungsweise 3. Grades heißen lineare, quadratische beziehungsweise kubische Gleichungen. Quadratische Gleichungen können mit der pq-Formel oder der Mitternachtsformel gelöst werden, Gleichungen 3. Grades mit der cardanischen Formel (nach Gerolamo Cardano, 1501-1576). Für Gleichungen 4. Grades entdeckte Ferrari, ein Schüler Cardanos eine (für die Praxis ungeeignete) Lösungsformel. Für algebraische Gleichungen höheren Grades gibt es keine allgemeine Lösungsformel (Beweis mit Hilfe der Galoistheorie).
1799 bewies Carl Friedrich Gauß den Fundamentalsatz der Algebra: "Jede algebraische Gleichung n-ten Grades (n > 0) besitzt mindestens eine komplexe Lösung. Zählt man eventuell vorkommende Vielfachheiten der Nullstellen entsprechend mehrfach, so hat die Gleichung genau n Lösungen".
Wikimedia Foundation.