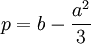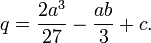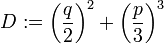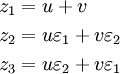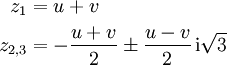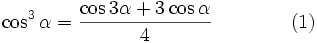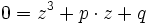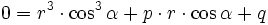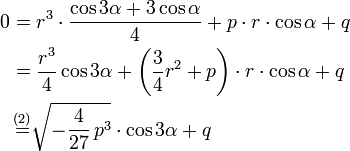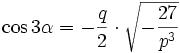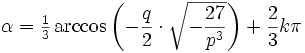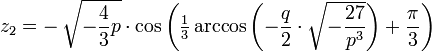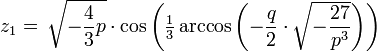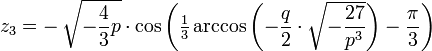- Cardanische Formel
-
Die cardanischen Formeln sind Formeln zur Lösung reduzierter kubischer Gleichungen (Gleichungen 3. Grades). Sie wurden, zusammen mit Lösungsformeln für quartische Gleichungen (Gleichungen 4. Grades), erstmals 1545 von dem Mathematiker Gerolamo Cardano in seinem Buch Ars magna veröffentlicht. Entdeckt wurde die Lösungsformel für kubische Gleichungen von Tartaglia; laut Cardano sogar noch früher durch Scipione del Ferro.
Die cardanischen Formeln waren eine wichtige Motivation für die Einführung der komplexen Zahlen, da man im Fall des casus irreducibilis durch das Ziehen einer Quadratwurzel aus einer negativen Zahl zu reellen Lösungen gelangen kann.
Die cardanischen Formeln besitzen heute für eine rein numerische Lösung kubischer Gleichungen kaum noch eine praktische Bedeutung, da sich die Lösungen bequemer durch das Newton-Verfahren mittels elektronischer Rechner bestimmen lassen. Sie sind dagegen für eine exakte Berechnung der Lösungen in Radikalen von erheblicher Bedeutung. Der Nachweis, dass es keine entsprechenden Formeln für Gleichungen fünften und höheren Grades geben kann, hat allerdings die Entwicklung der Algebra entscheidend beeinflusst (siehe Galoistheorie).
Inhaltsverzeichnis
Reduzierung der allgemeinen Gleichung dritten Grades
Die allgemeine Gleichung dritten Grades
- Ax3 + Bx2 + Cx + D = 0
mit reellen Zahlen A,B,C,D und
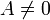 kann durch Division durch A zunächst in die Normalform
kann durch Division durch A zunächst in die Normalform- x3 + ax2 + bx + c = 0
gebracht werden. Mit Hilfe der Substitution
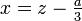 wird in der Normalform das quadratische Glied beseitigt und man erhält die reduzierte Form:
wird in der Normalform das quadratische Glied beseitigt und man erhält die reduzierte Form:- z3 + pz + q = 0,
wobei
und
Die reduzierte Form wird nun mit Hilfe der Cardanischen Formel aufgelöst und anschließend durch Rücksubstitution
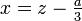 die Lösungen der ursprünglichen Gleichung bestimmt.
die Lösungen der ursprünglichen Gleichung bestimmt.Die Cardanische Formel zur Auflösung der reduzierten Form z³ + pz + q = 0
Im Unterschied zur Quadratischen Gleichung ist es bei der kubischen Gleichung erforderlich komplexe Zahlen zu betrachten, insbesondere auch dann, wenn alle drei Lösungen reell sind. Diese Tatsache hat im 16.Jh. zur Anerkennung der komplexen Zahlen geführt.
Die drei Lösungen ergeben sich durch z = u + v mit
![u = \sqrt[3]{-\frac{q}2 + \sqrt{D}}](/pictures/dewiki/54/6994d112110db3af6147fe29b997ecae.png) und
und ![v = \sqrt[3]{-\frac{q}2 - \sqrt{D}}](/pictures/dewiki/102/f9f1168bbd4ff0640dd9f792701c2a81.png) , wobei
, wobeidie Diskriminante der reduzierten Form ist. Die beiden komplexen 3. Wurzeln u und v müssen dabei so gewählt werden, dass die Nebenbedingung
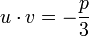 erfüllt ist (dadurch gibt es statt 9 nur 3 Paare (u,v).
erfüllt ist (dadurch gibt es statt 9 nur 3 Paare (u,v).Die beiden anderen dritten Wurzeln ergeben sich dann jeweils durch Multiplikation mit den beiden primitiven dritten Einheitswurzeln
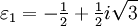 und
und 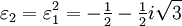 . Wegen der Nebenbedingung ergeben sich die drei Lösungen der reduzierten Form zu
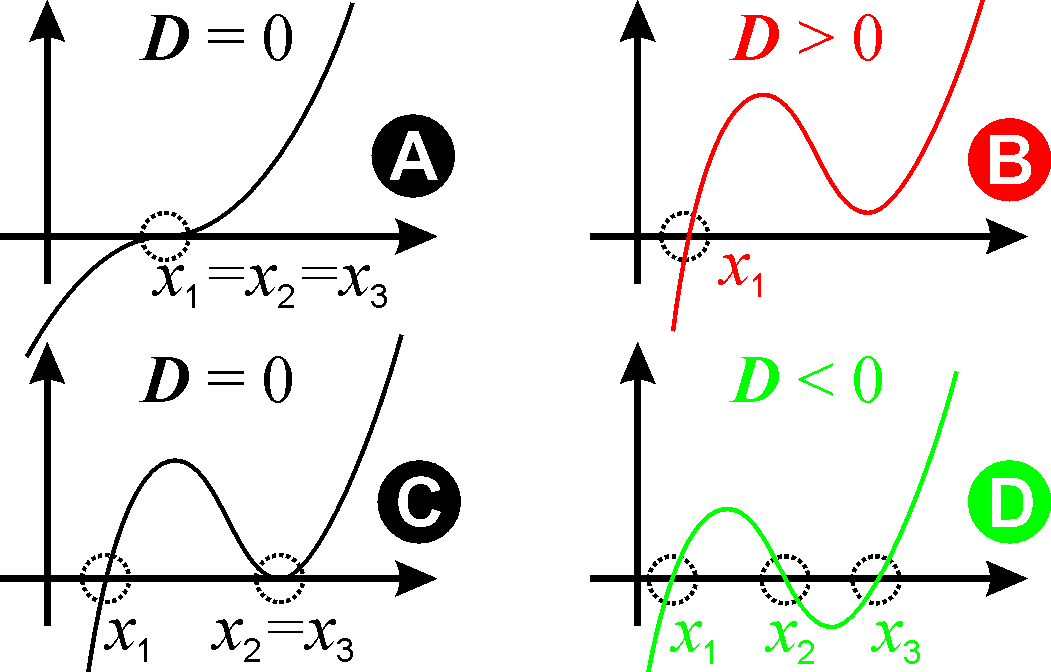
. Wegen der Nebenbedingung ergeben sich die drei Lösungen der reduzierten Form zuDas Lösungsverhalten hängt entscheidend vom Vorzeichen der Diskriminante ab:
- D > 0: Es gibt genau eine reelle Lösung und zwei echt komplexe Lösungen (Grafik: Fall B).
- D = 0: Es gibt entweder eine doppelte reelle Lösung und eine einfache reelle Lösung (Fall C) oder eine dreifache reelle Lösung (Fall A).
- D < 0: Es gibt drei verschiedene reelle Lösungen (Fall D).
Im Fall D > 0 gibt es für den Verlauf des zugehörigen Graphen zwei Möglichkeiten: entweder (Fall B) oder streng monoton wachsend (nicht im Bild dargestellt).
D > 0
Man wählt für u und v jeweils die reellen Wurzeln. Es gibt genau eine reelle und zwei konjugiert komplexe Lösungen, die nach den obigen Formeln durch
gegeben sind.
Allerdings ist das Ausziehen der Kubikwurzeln nicht immer so einfach. Cardano führt als Beispiel an: z3 + 6z − 20 = 0. Hierbei wählen wir
![u=\sqrt[3]{10 + \sqrt{108}} = 1+\sqrt3](/pictures/dewiki/54/6fb5ec47c9656820df31fbdc290fbc58.png) und
und ![v=\sqrt[3]{10 - \sqrt{108}} = 1-\sqrt3](/pictures/dewiki/48/087dd8892df94ee2ff2379021e4d75e1.png) reell. Somit ergibt sich z1 = 2 und
reell. Somit ergibt sich z1 = 2 und 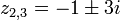 . Auf die Techniken zum Ausziehen von verschachtelten Wurzeln sei auf die Fachliteratur verwiesen.
. Auf die Techniken zum Ausziehen von verschachtelten Wurzeln sei auf die Fachliteratur verwiesen.D = 0
In diesem Fall wählt man u = v reell. Nach den obigen Formeln gibt es dann eine einfache reelle Lösung
![z_1 = 2u = \sqrt[3]{-4q} = \frac{3q}p](/pictures/dewiki/99/c9b0735fc25d87a2601d8a50f58bda17.png) ,
,
und eine doppelte reelle Lösung
![z_{2,3} = -u = \sqrt[3]{\frac{q}2} = -\frac{3q}{2p}](/pictures/dewiki/56/8d976f36d7801442fdf4426e2fe4bca7.png) .
.
Ist p = q = 0, so ist z = 0 die einzige (dreifache) Lösung.
D < 0 (casus irreducibilis)
Man wählt u und v jeweils konjugiert komplex zueinander, so ergeben sich dann durch
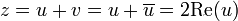 drei verschiedene reelle Lösungen.
drei verschiedene reelle Lösungen.Bei der Bestimmung von u müssen jedoch dritte Wurzeln aus echt komplexen Zahlen (z.B. mit Hilfe des Satzes von de Moivre) berechnet werden. Deshalb wird dieser Fall casus irreducibilis genannt. Mithilfe der trigonometrischen Funktionen können die Lösungen jedoch auch reell berechnet werden: Nach den Additionstheoremen, gilt für alle α die Beziehung
Schreibt man
mit Hilfe des Ansatzes
 um, ergibt sich
um, ergibt sichSetzt man hierin
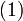 ein, dann entsteht
ein, dann entstehtDabei wurde
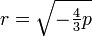 gewählt, so dass der Klammerausdruck in (2) verschwindet. Es ergibt sich
gewählt, so dass der Klammerausdruck in (2) verschwindet. Es ergibt sichmit ganzen Zahlen k.
Einsetzen in
 liefert mit k = − 1,0,1 die folgenden drei Lösungen:
liefert mit k = − 1,0,1 die folgenden drei Lösungen:Komplexe Koeffizienten
Das Vorgehen ist für komplexe Koeffizienten weitgehend analog, es gibt aber nur zwei Fälle:
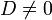 : Die oben für den Fall D > 0 angegebenen Formeln gelten analog; die beiden dritten Wurzeln sind dabei so zu wählen, dass ihr Produkt
: Die oben für den Fall D > 0 angegebenen Formeln gelten analog; die beiden dritten Wurzeln sind dabei so zu wählen, dass ihr Produkt 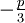 ergibt.
ergibt.- D = 0: Die oben für den Fall D = 0 angegebenen Formeln gelten unverändert.
Weblinks
Literatur
- Jörg Bewersdorff: Algebra für Einsteiger: Von der Gleichungsauflösung zur Galois-Theorie, Wiesbaden 2004, ISBN 3528131926, Einführung
- Heinrich Dörrie: Kubische und biquadratische Gleichungen, München 1948
- Ludwig Matthiessen: Grundzüge der antiken und modernen Algebra der litteralen Gleichungen, Leipzig 1896, Dokumenten-Server
- Peter Pesic: Abels Beweis, Springer 2005, ISBN 3-540-22285-5. Die Geschichte rund um die Lösungsformeln vom Grad 2 bis 4 und der komplette Beweis von Abel.
Wikimedia Foundation.