Kolinearitätsgleichung

Die Kollinearitätsgleichung beruht auf den mathematischen und geometrischen Grundlagen der kollinearen Abbildung. Ein typisches Beispiel für eine kollineare Abbildung ist die Zentralprojektion. Dabei werden Gerade wieder auf Gerade abgebildet, Teilungsverhältnisse bleiben erhalten.

Anwendungsgebiete der Kollinearitätsgleichung finden sich auf allen Gebieten der Optik und der optischen Bildaufzeichnung, speziell in der optischen Vermessung, der Photogrammetrie und anderer indirekter Messtechniken (z. B. Fließgeschwindigkeit eines Gewässers, Biegefestigkeit von Materialien). Meist wird von den aufgezeichneten Bildpunkten auf die Koordinaten der beobachteten Objektpunkt rückgerechnet. Bildpunkt, Projektionszentrum und beobachteter Objektpunkt liegen dabei auf einer Geraden.

Bei bekannten 3D-Koordinaten der Objektpunkte lassen sich deren Bildkoordinaten berechnen. Das entspricht der fotografischen Abbildung der Objektpunkte bei bekannter Kameraposition. Der Berechnung liegt das Modell einer Lochkamera zugrunde die im Idealfall die technische Umsetzung der Zentralprojektion darstellt. Als mathematische Formulierung der Zentralprojektion dienen die Kollinearitätsgleichungen für die Transformation der einzelnen Koordinaten der Punkte. Dabei wird im Wesentlichen mit einer 3x3 Rotationsmatrix multipliziert:

$x_c^{(i,j)} = s_x \cdot c \cdot \frac{r_{11}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{12}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{13}^{(i)} \cdot (z^{(j)}-z_0^{(i)})} {r_{31}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{32}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{33}^{(i)} \cdot (z^{(j)}-z_0^{(i)})}+ h_x + \Delta x \left( x_c^{(i,j)},y_c^{(i,j)} \right)$

$y_c^{(i,j)} = s_y \cdot c \cdot \frac{r_{21}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{22}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{23}^{(i)} \cdot (z^{(j)}-z_0^{(i)}) } {r_{31}^{(i)} \cdot (x^{(j)}-x_0^{(i)}) + r_{32}^{(i)} \cdot (y^{(j)}-y_0^{(i)}) + r_{33}^{(i)} \cdot (z^{(j)}-z_0^{(i)})}+ h_y + \Delta y \left( x_c^{(i,j)},y_c^{(i,j)} \right)$

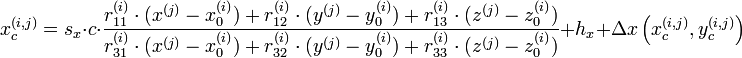
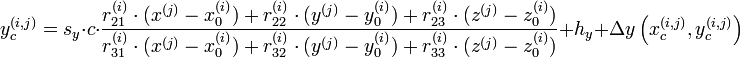
Die Symbole bedeuten dabei:

• i – Index zur Nummerierung der verschiedenen Kameras
• j – Index zur Nummerierung der verschiedenen Objekt- bzw. Bildpunkte
• c – Kammerkonstante, entspricht in etwa der Brennweite des Objektives
• r – 3×3 Rotationsmatrix zur Definition der Blickrichtung der Kamera
• (s_x,s_y)^T – Vektor zur Beschreibung der Asymmetrie der Bildpunkte von Matrixsensoren
• (x₀,y₀,z₀)^T – Vektor zur Definition des Projektionszentrums
• (x,y,z)^T – Vektor zur Definition der 3D-Koordinaten der Objektpunkte
• (h_x,h_y)^T – Vektor zur Definition der Lage des Bildhauptpunkts auf dem Film oder Sensor
• Δx und Δy – Funktionen zur Spezifizierung der Verzeichnungskorrekturen

Siehe auch

• kollinear