Gerade

Darstellung von Geraden im kartesischen Koordinatensystem

Eine gerade Linie oder kurz Gerade ist ein Element der Geometrie. Die kürzeste Verbindung zweier Punkte ist gerade und wird als Strecke bezeichnet. Eine gerade, unendlich lange, unendlich dünne und in beide Richtungen unbegrenzte Linie nennt man eine Gerade. Moderne axiomatische Theorien der Geometrie nehmen darauf jedoch keinen Bezug (Synthetische Geometrie). Für sie ist eine Gerade ein Objekt ohne innere Eigenschaften, lediglich die Beziehungen zu anderen Geraden, Punkten und Ebenen sind von Bedeutung. In der Analytischen Geometrie wird eine Gerade als eine Menge von Punkten realisiert. Genauer: In einem affinen Raum ist eine Gerade ein eindimensionaler affiner Unterraum.

Synthetische Geometrie

In seinen Elementen hat Euklid eine explizite Definition einer Geraden gegeben, die dem anschaulichen Bild entspricht. Für Sätze und ihre Beweise spielt diese Definition jedoch keine Rolle. Moderne Axiomensysteme verzichten daher auf eine solche Definition.

Eine Gerade ist in diesem Fall ein Begriff, auf den die einzelnen Axiome Bezug nehmen. Ein Beispiel ist das erste Axiom aus Hilberts Axiomensystem:

Zwei voneinander verschiedene Punkte P und Q bestimmen stets eine Gerade g.

Die Bedeutung des Begriffs Gerade ergibt sich aus der Gesamtheit der Axiome. Eine Interpretation als eine unendlich lange, unendlich dünne Linie ist nicht zwingend, sondern nur eine Anregung, was man sich anschaulich darunter vorstellen könnte.

In der projektiven Ebene sind die Begriffe Punkt und Gerade sogar vollständig austauschbar (Dualität). Damit ist es hier möglich, sich eine Gerade als unendlich klein und einen Punkt als unendlich lang und unendlich dünn vorzustellen.

Analytische Geometrie

In der analytischen Geometrie wird der geometrische Raum als n-dimensionaler Vektorraum über einem Körper K dargestellt. Eine Gerade wird dabei als eindimensionaler affiner Unterraum dieses Vektorraums definiert, d. h. als Nebenklasse eines eindimensionalen linearen Unterraumes.

In drei Dimensionen über dem Körper der reellen Zahlen erfüllt die Analytische Geometrie alle Bedingungen, die Hilbert in seinem Axiomensystem der Geometrie voraussetzt. In diesem Fall ist eine Gerade somit auch eine Gerade im Sinne Hilberts.

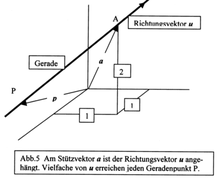
Man benötigt lediglich die Lage zweier Punkte, um eine Gerade zu beschreiben. Einer der Punkte dient dabei als "Stütze" der Geraden, auf ihm "liegt" sie sozusagen auf. Der zweite Punkt zeigt die Richtung der Geraden an. Die Richtung wird dabei durch den Vektor vom "Stützpunkt" zum "Richtungspunkt" angegeben. Die Gerade definiert sich dann folgender Maßen:

Veranschaulichung des Stütz- und Richtungsvektors

$g : \vec{x} = \overrightarrow{OP_1} + \lambda \overrightarrow{P_1 P_2}$

• $\vec{x}$ beschreibt dabei den allgemeinen Ortsvektor aller Punkte auf g
• $\overrightarrow{OP_\mathrm{1}}$ ist der Ortsvektor des Stützpunktes
• $\overrightarrow{P_\mathrm{1}P_\mathrm{2}}$ ist der Richtungsvektor von P₁ zu P₂
• λ ist der Skalar des Richtungsvektors

Die affine Hülle von zwei verschiedenen Vektoren x und y

$\{\lambda x + \mu y|\lambda, \mu \isin K, \lambda + \mu = 1\}$

ist ebenfalls eine Gerade.

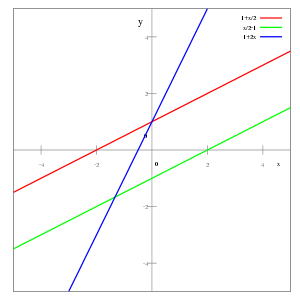
Auch der Lösungsraum eines (inhomogenen) linearen Gleichungssystems mit n − 1 linear unabhängigen Gleichungen ist ein affiner Unterraum der Dimension Eins und somit eine Gerade. In zwei Dimensionen kann eine Gerade folglich durch eine Geradengleichung

αx + βy = γ

angegeben werden, wobei $\alpha, \beta, \gamma \isin K$ und α oder β ungleich Null sein muss. Ist β ungleich 0, so spricht man von einer linearen Funktion auf K.

Kürzester Weg

Im reellen euklidischen Raum liegt der kürzeste Weg zwischen zwei Punkten auf einer Geraden. Verallgemeinert man diese Eigenschaft der Geraden auf gekrümmten Räumen (Mannigfaltigkeiten), so gelangt man zum Begriff der geodätischen Linie, kurz Geodäte.

Bestimmung der Gleichung einer Geraden in der Ebene

Die Gleichung einer Geraden in der Ebene kann man auf drei verschiedenen Weisen bestimmen:

Punkt-Richtung-Gleichung:

Gegeben sind ein Punkt P₀(x₀ | y₀) und der Neigungswinkel (Anstiegswinkel) α.

$y-y_0 = \tan(\alpha)\cdot(x-x_0)$

Gegeben sind ein Punkt P₀(x₀ | y₀) und die Steigung (der Anstieg) m.

$y-y_0 = m \cdot (x-x_0)$

Zwei-Punkte-Gleichung:

Gegeben sind zwei Punkte P₁(x₁ | y₁) und P₂(x₂ | y₂).

$y-y_1 = \frac{y_2-y_1}{x_2-x_1} \cdot (x-x_1)$

Bestimmung der Gleichung einer Geraden im dreidimensionalen Raum

Zwei-Punkte-Gleichung:

Gegeben sind zwei Punkte P₁(x₁ | y₁ | z₁) und P₂(x₂ | y₂ | z₂).

$\begin{pmatrix} x\\y\\z \end{pmatrix} = \begin{pmatrix} x_1\\y_1\\z_1 \end{pmatrix} + \lambda \begin{pmatrix} x_2-x_1\\y_2-y_1\\z_2-z_1 \end{pmatrix}$

Der Parameter λ kann alle reellen Zahlen als Wert annehmen.

Lage zweier Geraden zueinander

Zwei Geraden können folgende Lagebeziehungen zueinander haben. Sie können:

• Gleich sein: Beide Geraden haben alle Punkte gemeinsam
• Einen Schnittpunkt besitzen: Beide Geraden haben genau einen Punkt gemeinsam (speziell: senkrecht zueinander)
• Zueinander echt parallel sein: Beide Geraden haben keinen Punkt gemeinsam und lassen sich durch eine Verschiebung ineinander überführen.
• Zueinander windschief sein: Beide Geraden haben keinen Punkt gemeinsam, aber lassen sich nicht durch eine Verschiebung allein ineinander überführen (ab mindestens drei Dimensionen)

Im Sinne der Theorie der Relationen spricht man auch von Parallelität, wenn beide Geraden identisch sind, insbesondere ist jede Gerade zu sich selbst parallel. Zur Präzisierung unterscheidet man dann zwischen echt parallel und identisch.

Weblinks

• Eric W. Weisstein: Line. In: MathWorld. (englisch)