- Verzeichnung
-
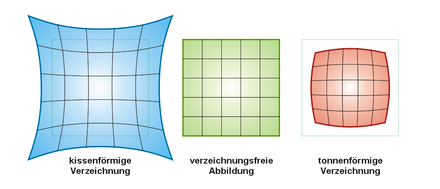
Die Verzeichnung oder optische Verzerrung ist ein geometrischer Abbildungsfehler optischer Systeme, der zu einer lokalen Veränderung des Abbildungsmaßstabes führt. Die Maßstabsänderung beruht auf einer Änderung der Vergrößerung mit zunehmendem Abstand des Bildpunktes von der optischen Achse. Die Verzeichnung ist daher rotationssymmetrisch um einen Punkt, der auch Verzeichnungszentrum genannt wird.
Nimmt die Vergrößerung zu den Rändern des Bildfelds zu, dann wird ein Quadrat kissenförmig verzeichnet. Im umgekehrten Fall spricht man von tonnenförmiger Verzeichnung. Es können auch Verzeichnungen höherer Ordnung auftreten, und die Überlagerung verschiedener Ordnungen kann zu einer wellenförmigen Abbildung gerader Linien führen („wellenförmige Verzeichnung“).
 Aufnahme durch ein Fischaugenobjektiv mit starker tonnenförmiger Verzeichnung
Aufnahme durch ein Fischaugenobjektiv mit starker tonnenförmiger Verzeichnung
Bei optischen Geräten für den alltäglichen Gebrauch ist die Verzeichnung kein merklicher Nachteil und wird daher in Kauf genommen. So haben Brillen für Kurzsichtige zum Rand hin eine stark tonnenförmige Verzeichnung. Bei Geräten mit mehreren Linsen, etwa bei Fernrohren, kann die Verzeichnung durch optische Kompensation gering gehalten werden:
- Verwendung von verschieden gekrümmten und unterschiedlich dicken Linsen
- Glassorten (Kronglas, Flintglas) mit unterschiedlicher Brechzahl für die einzelnen Linsen.
Diese verzeichnungsfreien Optiken nennt man orthoskopische Linsensysteme. Bei visuell genutzten Optiken wird jedoch nicht selten eine kissenförmige Verzeichnung absichtlich implementiert, um den störenden Globuseffekt zu eliminieren.
Werden fotografische Abbildungen für präzise Messungen verwendet, so sind möglichst korrigierte Linsensysteme erforderlich. Darüber hinaus wird die restliche Verzeichnung messtechnisch bestimmt und bei der Auswertung des Bildes rechnerisch korrigiert.
Die Verzeichnung eines Objektivs darf nicht mit der perspektivischen Verzerrung verwechselt werden, die daher kommt, dass man das Bild nicht in dem gleichen Blickwinkel betrachtet, in dem das Motiv von der Kameraposition aus zu sehen war.
Inhaltsverzeichnis
Korrektur von Verzeichnungen
Speziell für die Bildmessung in der Photogrammetrie sind Methoden entwickelt worden, um die Verzeichnung eines Objektivs zu modellieren und zu berechnen.
Durch Umkehrung dieser Modelle kann man die tatsächliche Verzerrung eines Bildes korrigieren und ein entzerrtes Bild berechnen.
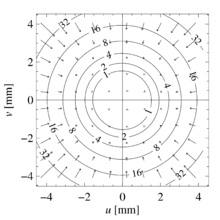
Das rechts stehende Bild zeigt die Verzeichnung eines 20-mm-Objektivs bei Fokussierung auf einen Meter Entfernung. Die Zahlen an den Isolinien geben den Betrag der Korrektur in Mikrometern an. Die Länge der Pfeile entspricht der fünfzehnfachen Länge der Korrektur. Die Koordinaten u und v sind die Bildkoordinaten bezogen auf die Bildmitte.
Verzeichnungen in Panoramafotografien
Die Fluchtpunktkonstruktion mithilfe von Geraden funktioniert in Bildern, in denen das dargestellte Objekt lediglich einen kleinen Teil des Sehfeldes ausfüllt. Auf Fotos bezogen sind dies Tele- oder Zoomaufnahmen mit langer Brennweite. Sollen jedoch Weitwinkelabbildungen dargestellt werden, versagt diese Technik aufgrund der wahrzunehmenden Verzeichnungen.
In solchen Fällen ist aus der Linie ein Bogen folgender Form zu konstruieren:

Erläuterungen zum Diagramm
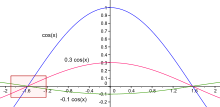
Der blaue Graph ist die Grundfunktion. Diese wird durch den Formelparameter H in der Höhe beeinflusst. Dadurch entstehen beispielsweise die Ober- und Unterkante einer endlosen Mauer; hier rot dargestellt. Diese wird auch durch entsprechende Panoramafotografien so dargestellt.
Im Diagramm ist hier von Fluchtpunkt zu Fluchtpunkt ein 180°-Schwenk dargestellt. Steht man dicht vor einer imaginären, endlosen Mauer und blickt zu deren linken Ende, so laufen hier Ober- und Unterkante im Fluchtpunkt zusammen. Dreht man sich nun zur anderen Seite, also nach rechts, so laufen hier ebenfalls Ober- und Unterkante in einem anderen, um 180° versetzten Fluchtpunkt zusammen. Da die parallelen Mauerober- und -unterkanten gemäß unserer Wahrnehmung in zwei Punkten zusammenlaufen und zwischendurch voneinander entfernt sind, müssen sie je einen Bogen beschreiben, wenn sie im Bild nicht abknicken sollen.
In dem grünen Rahmen ist beispielhaft ein Teil der Graphen eingerahmt, der der üblichen Fluchtpunktdarstellung entspricht; das heißt, er besteht annähernd aus Geraden.
Dies ist der Fall, da der Sinus kleiner Winkel ungefähr gleich dem Verhältnis von Gegenkathete zu Hypotenuse ist (sin(x)≈x für kleine |x|).
Im Bild lässt sich eindeutig die beschriebene Krümmung der Häuseroberkanten sowie die negative Krümmung ihrer Reflexion im Wasser erkennen.
Auch die Kante der Mauer, auf der der Fotograf stand, folgt dem beschriebenen Bogen (nicht vollständig sichtbar im Bild) und wirkt am linken oder rechten Rand wie eine Gerade aus der Parallelkonstruktion. Jedes einzelne kleine Haus übrigens auch, aber in ihrer Gesamtheit ergibt sich diese signifikante Krümmung.
In vertikaler sowie in allen anderen Richtungen besteht diese Krümmung ebenfalls, so dass sich in extremen Fischaugenobjektiv-Aufnahmen das gesamte Bild scheinbar zu einer Kugel zusammenrollt. Teilweise ist dieser Effekt in nebenstehender Aufnahme zu erkennen.
In 360°-Fischaugenobjektiv-Aufnahmen erhält man als Ergebnis ein kreisförmiges Bild, auf dem alles, was vom Standpunkt aus zu sehen ist, abgebildet wird. Bereiche, die sich bei diesen Aufnahmen hinter einem befinden, werden am Rand in extremster Verzeichnung dargestellt.
In Panoramaaufnahmen, wie oben zu sehen, tritt dieser Effekt in vertikaler Richtung ebenfalls auf, ist aber wegen der, im Verhältnis zur Breite, sehr geringen Bildhöhe zum einen nur sehr schwach wahrzunehmen und wird zum anderen durch Stitching-Programme, mit deren Hilfe solche Bilder erstellt werden, aus den zusammenzusetzenden Ausgangsbildern durch Verzeichnung dieser herausgerechnet, um ein nahtloses Aneinanderreihen der Bilder zu ermöglichen.
Herleitung der Krümmungsform
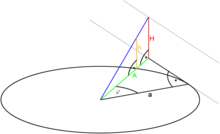
Zur Herleitung der Krümmungsform wird die Höhe (H) einer Imaginären Mauer als h auf die Oberfläche einer imaginären, senkrecht sehenden Röhre mit Radius a projiziert, in der der Betrachter steht. Gleichzeitig ist a aber auch der Abstand zur Mauer, die somit die imaginäre Röhre tangiert.
Außerdem sind:
- Tatsächliche Höhe = H
- Projizierte Höhe = h
- Kürzester Abstand zur Mauer = a
- Abstand zur Mauer in Blickrichtung = A
- Horizontaler Blickwinkel = φ
Winkelfunktion:
 [I]
[I]
Strahlensatz:
 [II]
[II]
Durch Einsetzen von [I] in [II] ergibt sich nach Vereinfachung:
- h = Hcos(φ)
Diese Krümmungsform der Verzeichnungslinien gilt wegen der Projektion auf einen Zylinder nur für Panoramabilder. Für Fischaugenobjektiv-Aufnahmen muss diese Projektion auf eine Kugel gerechnet werden.
Erwünschte Verzeichnung
In der Fotografie wird die Verzeichnung oft bewusst als künstlerisches Instrument eingesetzt.
Beim Fernsehen ist es oft nicht erwünscht, dass Zuschauer die reale räumliche Ausdehnung eines Studios erkennen können. Deshalb werden viele Studios - z.B. beim ZDF in Mainz - mit bogenförmigen Wänden oder gar kreisrund gebaut. Verwendet werden dann vorwiegend Weitwinkelobjektive. Deren Verzeichnung stört nicht wirklich - sie wird eher unbewusst wahrgenommen. Bei den Oberkanten der Wände - für Zuschauer die einzige "Marke" für die Größe des Raumes - kann die Objektivverzeichnung dann nicht von der "echten" Krümmung unterschieden werden; die Wand wirkt "endlos".
Literatur
- Fritz Deumlich, Rudolf Staiger: Instrumentenkunde der Vermessungstechnik, 9. Aufl., Wichmann, Heidelberg, 2001, ISBN 3-87907-305-8
- Karl Kraus: Photogrammetrie. de Gruyter, 2004, ISBN 3-11-017708-0
- Harry Paul: Lexikon der Optik, Spektrum Akademischer Verlag, Heidelberg 2003, ISBN 3-8274-1422-9
Siehe auch
Kategorien:- Optischer Fehler
- Photogrammetrie
- Optische Messtechnik
Wikimedia Foundation.