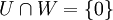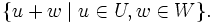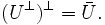Komplement (lineare Algebra)
- Komplement (lineare Algebra)
-
Ein Komplement oder ein komplementärer Unterraum ist im mathematischen Teilgebiet der linearen Algebra ein möglichst großer Unterraum, der einen vorgegebenen Unterraum nur im Nullpunkt schneidet. Der gesamte Vektorraum wird dadurch gewissermaßen in zwei unabhängige Teile zerlegt.
Definition: Komplement eines Untervektorraums
Es sei V ein Vektorraum über einem Körper K und U ein Unterraum von V. Dann heißt ein Unterraum W komplementär oder ein Komplement zu U, wenn die Bedingungen
und
erfüllt sind. Dabei steht U + W kurz für
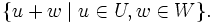
Man sagt dann auch: V ist die innere direkte Summe von U und W und schreibt  . Da V dann auch kanonisch isomorph zur äußeren direkten Summe von U und W ist, lässt man die Attribute „innere“ oder „äußere“ meist weg.
. Da V dann auch kanonisch isomorph zur äußeren direkten Summe von U und W ist, lässt man die Attribute „innere“ oder „äußere“ meist weg.
Eigenschaften
- Ist W ein Komplement von U in V so lässt sich jeder Vektor
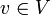 eindeutig als
eindeutig als
-
- v = u + w
- mit
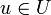 und
und 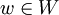 schreiben.
schreiben.
- Für die Dimensionen der entsprechenden Untervektorräume gilt
-

- Ist W ein Komplement zu U, so ist auch U ein Komplement zu W.
- Die Einschränkung der kanonischen Projektion
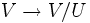 auf W ist ein Isomorphismus, siehe Faktorraum.
auf W ist ein Isomorphismus, siehe Faktorraum.
Definition: Orthogonales Komplement
Es sei V ein Vektorraum über einem Körper K, auf dem eine symmetrische oder alternierende Bilinearform oder eine hermitesche Sesquilinearform gegeben ist. Für einen Unterraum 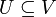 heißt
heißt

das orthogonale Komplement oder der Orthogonalraum von U in V. Man beachte, dass es im Allgemeinen kein Komplement von U im oben definierten Sinne ist. Der Dualitätssatz besagt jedoch, dass, falls V endlichdimensional und s sowohl auf V als auch auf dem Unterraum U nicht ausgeartet ist, 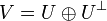 gilt.
gilt.
Die letzte Bedingung ist beispielsweise für positiv definite Skalarprodukte auf reellen oder komplexen Vektorräumen erfüllt.
Orthogonales Komplement in Hilberträumen
Ist V ein Hilbertraum und s das Skalarprodukt des Hilbertraums, so ist das orthogonale Komplement eines Unterraumes U ein Komplement seines Abschlusses  , d.h.
, d.h.

Das orthogonale Komplement ist stets abgeschlossen, und es gilt
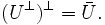
Siehe auch
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Kegel (Lineare Algebra) — In der linearen Algebra ist ein (linearer) Kegel eine Teilmenge eines Vektorraums, die abgeschlossen bzgl. Multiplikation mit positiven Skalaren ist. Inhaltsverzeichnis 1 Definition 2 Spitze und stumpfe Kegel 3 Ko … Deutsch Wikipedia
Komplement — (lateinisch: complementum = „Ergänzung“, „Vervollständigung[smittel]“ – complere = „erfüllen“, „ergänzen“) steht für folgende Begriffe: Komplementäres Gut, in den Wirtschaftswissenschaften ein bestimmtes Gut Komplementsystem, in der Medizin … Deutsch Wikipedia
Orthogonales Komplement — Ein Komplement oder ein komplementärer Unterraum ist im mathematischen Teilgebiet der linearen Algebra ein möglichst großer Unterraum, der einen vorgegebenen Unterraum nur im Nullpunkt schneidet. Der gesamte Vektorraum wird dadurch gewissermaßen… … Deutsch Wikipedia
Schur-Komplement — In der linearen Algebra bezeichnet das Schur Komplement eine Matrix, die sich aus den einzelnen Blöcken einer größeren Matrix berechnet. Das Schur Komplement ist nach Issai Schur benannt. Inhaltsverzeichnis 1 Definition 2 Interpretation als… … Deutsch Wikipedia
AF-C*-Algebra — AF C* Algebren, oder kürzer AF Algebren, bilden eine im mathematischen Teilgebiet der Funktionalanalysis betrachtete Klasse von C* Algebren, die sich aus endlichdimensionalen C* Algebren aufbauen lassen, AF steht für approximately finite (fast… … Deutsch Wikipedia
Quotientenvektorraum — Der Faktorraum ist ein Begriff aus der linearen Algebra, einem Teilgebiet der Mathematik. Er ist derjenige Vektorraum, der als Bild einer Parallelprojektion entlang eines Unterraumes entsteht. Inhaltsverzeichnis 1 Definition 2 Eigenschaften 3… … Deutsch Wikipedia
Projektionsabbildung — In der Mathematik ist eine Projektion oder ein Projektor eine idempotente lineare Abbildung eines Vektorraumes V in sich selbst. Das Bild einer Projektion ist entweder ein niedrigerdimensionaler Teilraum von V oder V selbst. Bei geeigneter Wahl… … Deutsch Wikipedia
Codimension — Die Kodimension bezeichnet in verschiedenen Bereichen der Mathematik das Komplement zur Dimension: Beispielsweise ist im dreidimensionalen Raum die Summe aus Dimension und Kodimension eines Objektes gleich 3. Definition Es sei V ein Vektorraum… … Deutsch Wikipedia
Win Ali — WinAli ist ein Modell Assembler (siehe auch Assemblersprache) für Windows und DOS. Der generierte Maschinencode wird mit einem Modellrechner ausgeführt, der eine Emulation eines echten Prozessors darstellt. WinAli ist dazu gedacht, um Assembler… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
 . Da V dann auch kanonisch isomorph zur äußeren direkten Summe von U und W ist, lässt man die Attribute „innere“ oder „äußere“ meist weg.
. Da V dann auch kanonisch isomorph zur äußeren direkten Summe von U und W ist, lässt man die Attribute „innere“ oder „äußere“ meist weg.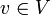 eindeutig als
eindeutig als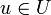 und
und 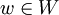 schreiben.
schreiben.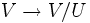 auf W ist ein Isomorphismus, siehe Faktorraum.
auf W ist ein Isomorphismus, siehe Faktorraum.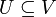 heißt
heißt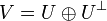 gilt.
gilt. , d.h.
, d.h.