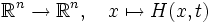Adhärenzpunkt — Dies ist ein Glossar einiger Begriffe, die in dem Bereich der Mathematik vorkommen, der als Topologie bekannt ist. Dieses Glossar besteht aus zwei Teilen. Der erste Teil beschäftigt sich mit allgemeinen Konzepten und der zweite Teil erklärt Typen … Deutsch Wikipedia
Kontrahierbarkeit — Im mathematischen Teilgebiet der Topologie heißt ein topologischer Raum X kontrahierbar oder zusammenziehbar, wenn er homotopieäquivalent zu einem einpunktigen Raum ist, d.h. wenn es eine stetige Abbildung gibt, für die H(x,0) = x für alle und… … Deutsch Wikipedia
Satz von Seifert-van Kampen — Der Satz von Seifert van Kampen (benannt nach Herbert Seifert und Egbert van Kampen) gehört zum Gebiet der algebraischen Topologie. Er macht eine Aussage über die Struktur der Fundamentalgruppe eines topologischen Raumes X, indem man die… … Deutsch Wikipedia
Sternförmig — sternförmige Menge mit Zentrum x0, ihr Inneres (grün) ist ein Sterngebiet In der Mathematik versteht man unter einer sternförmigen Menge eine Teilmenge M des , zu der es einen Punkt p gibt (ein Sternzentrum), von dem aus alle Punkte der Menge… … Deutsch Wikipedia
Sternförmiges Gebiet — sternförmige Menge mit Zentrum x0, ihr Inneres (grün) ist ein Sterngebiet In der Mathematik versteht man unter einer sternförmigen Menge eine Teilmenge M des , zu der es einen Punkt p gibt (ein Sternzentrum), von dem aus alle Punkte der Menge… … Deutsch Wikipedia
Sternzentrum — sternförmige Menge mit Zentrum x0, ihr Inneres (grün) ist ein Sterngebiet In der Mathematik versteht man unter einer sternförmigen Menge eine Teilmenge M des , zu der es einen Punkt p gibt (ein Sternzentrum), von dem aus alle Punkte der Menge… … Deutsch Wikipedia
Topologie Glossar — Dies ist ein Glossar einiger Begriffe, die in dem Bereich der Mathematik vorkommen, der als Topologie bekannt ist. Dieses Glossar besteht aus zwei Teilen. Der erste Teil beschäftigt sich mit allgemeinen Konzepten und der zweite Teil erklärt Typen … Deutsch Wikipedia
Zusammenziehbar — Im mathematischen Teilgebiet der Topologie heißt ein topologischer Raum X zusammenziehbar oder kontrahierbar, wenn er homotopieäquivalent zu einem einpunktigen Raum ist, d.h. wenn es eine stetige Abbildung gibt, für die H(x,0) = x für alle und… … Deutsch Wikipedia
Konkave Menge — eine konvexe Menge eine nichtkonvexe Menge In der Mathematik heißt eine geometrische Figur oder allgemeiner eine Teilmenge eines … Deutsch Wikipedia
Konvexe Menge — eine konvexe Menge eine nichtkonvexe Menge In der … Deutsch Wikipedia
 und
und mit einem festen
mit einem festen 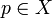
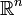 ist zusammenziehbar: Setze
ist zusammenziehbar: Setze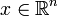 und
und 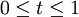 .
.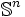 (oder allgemeiner: eine entsprechende Sphäre mit festem Radius) ist nicht zusammenziehbar. Jedoch für
(oder allgemeiner: eine entsprechende Sphäre mit festem Radius) ist nicht zusammenziehbar. Jedoch für 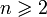 einfach zusammenhängend.
einfach zusammenhängend.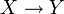 heißt nullhomotop (auch zusammenziehbar oder kontrahierbar), wenn sie homotop zu einer konstanten Abbildung ist.
heißt nullhomotop (auch zusammenziehbar oder kontrahierbar), wenn sie homotop zu einer konstanten Abbildung ist.
![H\colon X\times[0,1]\to X](/pictures/dewiki/98/b0c1a573265a525fa4bdd2c024004632.png)