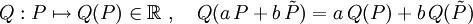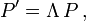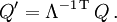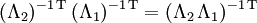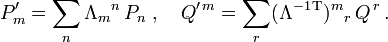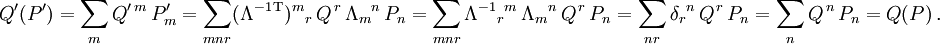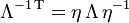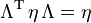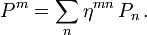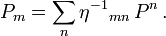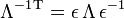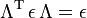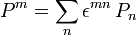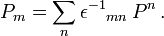Kontravarianz (Physik)

Kovariant sind in der Physik Größen, die unter einer Gruppe von Transformationen wie beispielsweise Lorentz-Transformationen oder Galilei-Transformationen linear transformieren: die transformierten Größen sind Linearkombinationen der ursprünglichen.

So sind beispielsweise die Beschleunigung und die Kraft und daher die newtonschen Bewegungsgleichungen kovariant bei Galilei-Transformationen. In gleichem Sinn sind die Einstein-Gleichungen kovariant unter beliebigen Koordinatentransformationen oder die Dirac-Gleichung kovariant unter Lorentztransformationen^[1].

Die linke Seite der Klein-Gordon-Gleichung für ein Skalarfeld ändert sich unter Lorentztransformationen nicht, sie ist spezieller invariant oder skalar.

Kovariante Größen sind nach der Transformation genau dann null, wenn sie vor der Transformation null waren.

Ko- und Kontravariant

In einem engeren Wortsinn bezeichnet kovariant in der mathematischen Physik Größen, die so wie Differentialformen transformieren. Diese kovarianten Größen P bilden einen Vektorraum 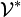$\mathcal V^*$, auf dem eine Gruppe von linearen Transformationen wirkt.

Die Menge der linearen Abbildungen der kovarianten Größen in die reellen Zahlen

$Q:P\mapsto Q(P)\in\mathbb R\ ,\quad Q(a\,P+b\,\tilde P)=a\,Q(P)+b\,Q(\tilde P)$

bildet den zu 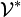$\mathcal V^*$ dualen Vektorraum 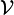$\mathcal V$. Schreiben wir die transformierten, kovarianten Größen 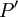$P^\prime$ mit einer Matrix Λ als

$P^\prime=\Lambda\,P\,,$

dann definiert 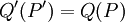$Q^\prime(P^\prime)=Q(P)$ das kontravariante oder kontragrediente Transformationsgesetz des Dualraumes

$Q^\prime=\Lambda^{-1\,\text{T}}\,Q\,.$

Wegen

$(\Lambda_2)^{-1\,\text{T}}\,(\Lambda_1)^{-1\,\text{T}}=(\Lambda_2\,\Lambda_1)^{-1\,\text{T}}$

genügt die kontravariante Transformation derselben Gruppenverknüpfung wie die kovariante Transformation.

Tensoren aus dem u-fachen Tensorprodukt von 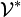$\mathcal V^*$ mit dem o-fachen Tensorprodukt von 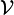$\mathcal V$ heißen u-fach kovariant und o-fach kontravariant.

In Indexschreibweise macht man an der Indexstellung mit unten und oben stehenden Indizes deutlich, ob es sich um die Komponenten eines kovarianten oder eines kontravarianten Vektors handelt,

$P^{\prime}_m=\sum_n\Lambda_m{}^ n\,P_n\ ,\quad Q^{\prime\,m} = \sum_r(\Lambda^{-1\,\text{T}})^m{}_r\,Q^{\,r}\,.$

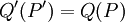Dass $Q^\prime(P^\prime) = Q(P)$ gilt, zeigen die Rechenschritte

$Q^\prime(P^\prime) =\sum_m Q^{\prime\,m}\, P^{\prime}_m = \sum_{mnr}(\Lambda^{-1\,\text{T}})^m{}_r\,Q^{\,r}\,\Lambda_m{}^n\,P_n = \sum_{mnr}\Lambda^{-1}{}_r{}^m\,\Lambda_m{}^n\,Q^{\,r}\,P_n = \sum_{nr}\delta_r{}^n\,Q^{\,r}\,P_n = \sum_n Q^{\,n}\,P_n = Q(P)\,.$

Indexziehen

Ist das kontravariante Transformationsgesetz dem kovarianten äquivalent und gilt für alle Λ der Transformationsgruppe

$\Lambda^{-1\,\text{T}}=\eta\,\Lambda\,\eta^{-1}$

mit einer invertierbaren, symmetrischen Matrix η = η^T, dann handelt es sich bei der Transformationsgruppe wegen

$\Lambda^{\text{T}}\,\eta\,\Lambda= \eta$

um eine Untergruppe der orthogonalen Gruppe, die die symmetrische Bilinearform 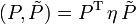$(P,\tilde P)=P^{\text{T}}\,\eta\,\tilde P$ invariant lässt. Dann definiert 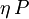$\eta \,P$ einen kontravarianten Vektor, wenn P ein kovarianter Vektor ist. In Indexschreibweise schreibt man für die Komponenten von 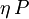$\eta \,P$ abkürzend

$P^m = \sum_n \eta^{mn}\,P_n\,.$

Dann gilt umgekehrt

$P_m = \sum_n \eta^{-1}{}_{mn}\,P^n\,.$

Diesen Zusammenhang der Komponenten des kovarianten Vektors P und des kontravarianten Vektors ηP nennt man Indexziehen.

Ist das kontravariante Transformationsgesetz dem kovarianten äquivalent und gilt für alle Λ der Transformationsgruppe

$\Lambda^{-1\,\text{T}}=\epsilon\,\Lambda\,\epsilon^{-1}$

mit einer invertierbaren, antisymmetrischen Matrix ε = − ε^T, dann handelt es sich bei der Transformationsgruppe wegen

$\Lambda^{\text{T}}\,\epsilon\,\Lambda= \epsilon$

um eine Untergruppe der symplektischen Gruppe, die die antisymmetrische Bilinearform 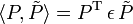$\langle P,\tilde P\rangle =P^{\text{T}}\,\epsilon\,\tilde P$ invariant lässt. Dann definiert 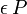$\epsilon \,P$ einen kontravarianten Vektor, wenn P ein kovarianter Vektor ist. In Indexschreibweise kann man für die Komponenten von 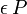$\epsilon \,P$ abkürzend

$P^m = \sum_n \epsilon^{mn}\,P_n$

schreiben. Dann gilt umgekehrt

$P_m = \sum_n \epsilon^{-1}{}_{mn}\,P^n\,.$

Dieser Zusammenhang der Komponenten des kovarianten Vektors P und des kontravarianten Vektors εP definiert das Indexziehen von Vektoren, die unter der symplektischen Gruppe transformieren.

Siehe auch

• Kovariante Ableitung

Bücher

• Peter Szekeres, A Course in Modern Mathematical Physics, Cambridge University Press, New York, 2004 ISBN 0-521-82960-7

Weblinks

• Norbert Dragon, Stichworte und Ergänzungen zu Rechenmethoden der Physik

Nachweise

1. ↑ James Bjorken und Sidney Drell: Relativistische Quantenmechanik, BI-Wissenschaftsverlag, Mannheim, 1990, (BI-Hochschultaschenbuch Band 98), ISBN 3-411-00098-8, Kapitel 2