Galilei-Transformation

Die Koordinatentransformation von einem Bezugssystem B₁ in ein anderes Bezugssystem B₂ nennt man Galilei-Transformation, wenn sich B₂ von B₁ nur durch eine räumliche Parallelverschiebung, eine Zeit-Translation, eine Drehung oder eine gleichförmig geradlinige Bewegung unterscheidet. Eine Galilei-Transformation ist also durch 10 Parameter festgelegt: 3 Koordinaten der Raumverschiebung, 1 der Zeitverschiebung, 3 des Bewegungsvektors und 3 der Drehung.

Gültigkeit der Galilei-Transformation

Klassische Mechanik

Die klassische Mechanik beginnt bereits vor Newton durch die Ideen des René Descartes. Im Gegensatz zur Scholastik des Mittelalters beschreibt sie Raum und Zeit aus Koordinatensystemen relativ zu einem willkürlich gewählten Ursprung.

Die Unabhängigkeit der Gesetze der Mechanik vom Bewegungszustand bei gleichförmiger Bewegung wurde erst in der klassischen Physik erkannt. Kräfte sind bei Isaac Newton nur von den Beschleunigungen abhängig, die sich unter Galilei-Transformationen nicht ändern. In der klassischen Mechanik behält das Prinzip uneingeschränkte Gültigkeit, man hielt es lange Zeit für a priori gegeben und unangreifbar.

Lorentz-Transformation

Die klassische Elektrodynamik bis zum Ende des 19. Jahrhunderts ging von einem Äther als Träger elektromagnetischer Wellen einschließlich des Lichts aus. Die Maxwellschen Gleichungen und die daraus resultierende Lichtgeschwindigkeit c als Ausbreitungsgeschwindigkeit der elektromagnetischen Wellen waren jedoch nicht vereinbar mit der Galilei-Transformation. Hendrik Antoon Lorentz, Joseph Larmor, und Henri Poincaré erkannten, dass man dieses Problem lösen könne, indem man die Galilei-Transformation durch die Lorentz-Transformation ersetzt. Dies führte schließlich zur speziellen Relativitätstheorie von Albert Einstein, welche allerdings eine Modifikation der Vorstellungen von Zeit und Raum erfordert.

Für Geschwindigkeiten, die sehr viel kleiner als die Lichtgeschwindigkeit von ca. 300.000 km/s sind, ist die Galilei-Transformation eine gute Näherung der Lorentz-Transformation. Die Galilei-Transformation ist der Grenzfall der Lorentz-Transformation für kleine Geschwindigkeiten.

Praktische Anwendung

Im Alltagsleben kann bei mechanischen Problemen fast immer die Galilei-Transformation angewendet werden, da die Korrektur in der Lorentz-Transformation bei irdischen Geschwindigkeiten sehr klein ist. Der Korrekturfaktor liegt oft unterhalb der Messbarkeitsgrenze. Selbst in der Himmelsmechanik unseres Plantensystems liegt dieser Faktor z. B. unter 10⁻⁸ für die schon recht große Umlaufgeschwindigkeit der Erde um die Sonne (etwa 30 km/s).

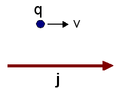
Ladung und Leiter
Ladung q und Leiter mit Strom j. Diese Konfiguration ist nicht Galilei-transformierbar.

Dem Anwendungsbereich komplett entziehen sich jedoch elektrodynamische Phänomene des Alltagslebens. Ein einfaches Beispiel eines geladenen Körpers, der an einem stromdurchflossenen Leiter vorbeifliegt, zeigt den Mangel auf:

• Eine Ladung q fliegt mit der anfänglichen Geschwindigkeit v an einem geraden stromdurchflossenen, aber ladungsneutralen, Leiter vorbei (siehe Bild). Der Strom im Leiter erzeugt ein Magnetfeld, welches die bewegte Ladung q durch die Lorentz-Kraft von ihrer gradlinigen Bewegung ablenkt. Führt man nun eine Galilei-Transformation durch, die in das Inertialsystem der Ladung zum Anfangszeitpunkt wechselt, so wirkt in diesem System keine Lorentz-Kraft, denn die Ladung befindet sich in Ruhe. Die Ladung sollte also an ihrem Ausgangspunkt verharren. Die Rücktransformation führt zu einer gradlinigen Bewegung im Widerspruch zur obigen Aussage, nach der die Ladung durch die Lorentz-Kraft beschleunigt wird. Erklärt werden kann dieses scheinbare Paradoxon erst mit der Lorentz-Transformation, bei der sich die Länge des Leiters im Inertialsystem der Ladung kontrahiert und der Leiter somit eine relative elektrische Ladung erhält. Das resultierende elektrische Feld ersetzt das ursprünglich magnetische. Hier wird auch die Verwandtschaft beider Felder etwas deutlich.

Galileitransformation und Erhaltungssätze

Die Naturgesetze ändern sich nicht unter Galileitransformation. Der Ausgang eines Experiments bleibt gleich, wenn man seinen Ort einer Galileitransformation unterzieht. Eine Verschiebung des Orts, oder in der Zeit, oder auch der Ausrichtung ändern nichts. So eine Invarianz wird auch Symmetrie genannt. Nach dem Noether-Theorem ist jede solche Symmetrie mit einem Erhaltungssatz verknüpft. Aus der Invarianz der Naturgesetze unter Galilei-Transformation folgen damit die Erhaltungssätze der klassischen Mechanik. Im einzelnen:

• Aus der Invarianz unter Verschiebung des Orts folgt die Impulserhaltung.
• Aus der Invarianz unter Verschiebung in der Zeit folgt die Energieerhaltung.
• Aus der Invarianz unter Drehung folgt die Drehimpulserhaltung.

Mathematische Beschreibung

Verschiebung entlang einer Achse

Eine besonders einfache Galileitransformation ist die Verschiebung des Ursprungs entlang der x-Achse eines kartesischen Koordinatensystems. Sie gibt an, wie man die Koordinaten x,y,z,t verändern muss, um ein physikalisches System von einem um die Strecke x₀ verschobenen Ursprung in den Koordinaten x',y',z',t' zu beschreiben. Die Koordinaten auf der y-Achse, der z-Achse und in der Zeit bleiben gleich. Zur x-Koordinate wird der Wert x₀ addiert. In Formeln also:

$x'=x + x_0, \quad y'=y,\quad z'=z,\quad \mathrm{und} \quad t'=t$

Allgemeinere Formen

Die Galilei-Transformation gilt auch

• für gleichförmige Geschwindigkeiten in beliebiger Richtung,
• wenn die Nullpunkte der Bezugssysteme nicht zusammenfallen,
• für unterschiedliche Zeitpunkte,
• und für gedrehte Bezugssysteme mit zeitlich konstanten Winkeln.

Vektorielle Schreibweise

Die drei Formeln für die Transformation der Ortskoordinaten lassen sich zu einer Gleichung für einen Ortsvektor zusammenfassen. Dies ist zunächst nur eine Abkürzung, erweist sich jedoch bei komplizierteren Transformationen als nützlich.

Setzt man

$\vec{s'}=\begin{pmatrix}x'\\y'\\z'\end{pmatrix},\quad \vec{s}=\begin{pmatrix}x\\y\\z\end{pmatrix} \quad \mathrm{und} \quad \vec{s_0}=\begin{pmatrix}x_0\\0\\0\end{pmatrix}$

so kann man die vier Gleichungen für die gleichförmige Verschiebung des Koordinatenursprungs entlang der x-Achse auch so schreiben:

$\vec{s'}=\vec{s} + \vec{s_0} \quad \mathrm{und} \quad t' = t$

Die erste Gleichung enthält dabei die drei Gleichungen für die Ortskoordinaten in vektorieller Schreibweise.

Gleichförmige Geschwindigkeiten in beliebiger Richtung

Die vektorielle Form gilt sofort auch für die Verallgemeinerung auf Geschwindigkeiten, die nicht parallel zur x-Achse erfolgen, wenn man setzt:

$\vec{v}=\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}$

Die Geschwindigkeit und ihre Komponenten müssen zeitlich konstant sein.

Die Nullpunkte der Bezugssysteme fallen nicht zusammen

Die Konstante

$\vec{s_0}=\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}$

wird eingeführt. Bei t=0 ist dies der Abstand der Nullpunkte der Bezugssysteme. Die Galilei- Transformation wird dann zu

$\vec{s'}=\vec{s}-t \cdot \vec{v} + \vec{s_0},\quad t'=t$.

Anschaulich bedeutet dies, dass ich dem Tischtennisspiel im Zug auch von der Ferne aus zuschauen kann.

Unterschiedliche Zeitpunkte

Die Zeit braucht nicht gleich zu sein, sondern kann um t₀ unterschiedlich sein.

$\vec{s'}=\vec{s}-t \cdot \vec{v} + \vec{s_0},\quad t'=t - t_0$.

Die Gesetze der Mechanik ändern sich nicht mit der Zeit.

Gedrehte Bezugssysteme

Die Koordinatenachsen der Bezugssysteme müssen nicht in dieselbe Richtung zeigen. Mathematisch müssen dann die Koordinaten umgerechnet werden, was ohne vektorielle Schreibweise zu recht langen Formeln führt.

Vektoriell kann man einfach eine Drehmatrix mit neun Zahlen verwenden. Da die Längen nicht geändert werden, müssen bestimmte Bedingungen an diese Matrix gestellt werden, so dass nur drei Parameter (z. B. Winkel) unabhängig sind. Die Schreibweise mit neun Zahlen ist aber trotzdem die einfachste:

$\mathbf{a}=\begin{pmatrix}a_{xx} & a_{xy} & a_{xz} \\ a_{yx} & a_{yy} & a_{yz} \\ a_{zx} & a_{zy} & a_{zz} \end{pmatrix}$

Eine gültige Drehmatrix ist z. B. (45° Winkel um die z-Achse)

$\mathbf{a}=\begin{pmatrix}\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}} & 0 \\ \sqrt{\frac{1}{2}} & \sqrt{\frac{1}{2}} & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Die Galilei-Transformation in ihrer allgemeinsten Form wird dann zu

$\vec{s'}=\mathbf{a} \cdot (\vec{s}-t \cdot \vec{v} + \vec{s_0}),\quad t'=t - t_0$.

Die allgemeine Form hat 10 Parameter (drei Drehwinkel, drei Abstandskoordinaten, drei Geschwindigkeitskomponenten und die Zeitverschiebung).

Anschaulich bedeutet dies, dass ich das Tischtennisspiel im Zug durch ein Fenster aus einem schräg fliegenden Flugzeug auf Film aufnehmen und mir dann z. B. eine Woche später anschauen kann. Die Gesetze der Physik haben sich in dieser Zeit nicht geändert.