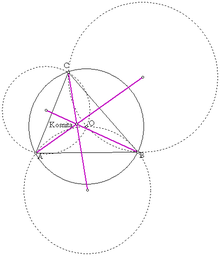
Kosnita-Punkt

Satz von Kosnita

Der Kosnita-Punkt ist einer der besonderen Punkte eines Dreiecks mit Kimberling-Nummer X(54). Er ist isogonal konjugiert zum Mittelpunkt des Feuerbach-Kreises.

Der Punkt hat seinen Namen nach dem Satz von Kosnita: Ist O der Mittelpunkt des Umkreises, dann ist das Dreieck, das von den Umkreismittelpunkten der Dreiecke OBC, AOC und ABO gebildet wird, perspektiv zu ABC. Das Perspektivitätszentrum ist der Punkt von Kosnita.

Koordinaten

Die baryzentrischen Koordinaten des Kosnita-Punktes sind

$\frac{\sin\alpha}{\cos(\beta-\gamma)} \, : \, \frac{\sin\beta}{\cos(\gamma-\alpha)} \, : \, \frac{\sin\gamma}{\cos(\alpha-\beta)}.$

Weblinks

• Eric W. Weisstein: Kosnita Point. In: MathWorld. (englisch)