Kubische Iterationen

Die Kubischen Iterationen fallen in das Gebiet der diskreten Dynamiken in der komplexen Ebene.

Julia-Mengen zu Polynomen

Jedes Polynom $p\in\mathbb C[X]$ definiert eine Abbildung der komplexen Ebene in sich selbst. Wählt man einen Startpunkt $z_0\in\mathbb C$, so kann man verfolgen, wohin dieser durch p transportiert wird. Wählt man rekursiv den jeweiligen Endpunkt als Anfangspunkt, so erhält man eine komplexwertige Folge $(z_k)_{k\in\N}$, bei z_k = p(z_{k − 1}). In der üblichen Notation für mehrfache Verkettungen einer Abbildung mit sich gilt also $(z_k)_{k\in\N}=\left(p^k(z_0)\right)_{k\in\N}$.

Man kann die Punkte z der komplexen Ebene nun danach einteilen, ob die Folge $\left(p^k(z)\right)_{k\in\N}$ beschränkt bleibt oder über alle Grenzen wächst. Die Menge

$\operatorname{Julia}_p:=\left\{z\in\mathbb C|\sup_{k\in\N}|p^{k}(z_0)|<\infty\right\}$

der Startpunkte mit beschränkten Iterationsfolge ist die Julia-Menge von p.

Mandelbrot-Mengen

Man kann nun die Polynome danach unterscheiden, ob deren Julia-Menge topologisch zusammenhängend ist oder nicht. Um daraus ein darstellbares Gebilde zu gewinnen, muss man eine durch höchstens drei reelle Parameter darstellbare Teilmenge in der Menge aller Polynome wählen. Um einen möglichst großen Überblick zu gewinnen, ist dabei zu vermeiden, dass Polynome mit ähnlichen Julia-Mengen in der Parametrisierung enthalten sind. Eine einfache Ähnlichkeit entsteht durch die Verschiebung oder allgemein lineare Transformation der Julia-Menge. Eine beschränkte Folge $(z_k)_{k\in\N}$ ergibt auch nach einer linearen Transformation w=qz+r, $q,r\in\mathbb C$, eine beschränkte Folge $(w_k)_{k\in\N}$. Ist q von Null verschieden, so gilt auch die umgekehrte Aussage.

Entstand die Folge $(z_k)_{k\in\N}$ durch eine polynomiale Dynamik p, so entsteht ebenfalls die Folge $(w_k)_{k\in\N}$ durch eine polynomiale Dynamik gleichen Grades. Das zugehörige Polynom ergibt sich aus dem Ausgangspolynom p nach

$w_{k+1}=q\,z_{k+1}+r=q\cdot p(z_k)+r=q\cdot p\left(q^{-1}\cdot(w_k-r)\right)+r$

als $p_{(q,r)}(X):=q\cdot p(q^{-1}\,(X-r))+r,\ d\in\mathbb C$. Jedes so entstehende Polynom heiße im Rahmen dieses Artikels linear äquivalent zu p(X).

Sei p(X) vom Grade d, $p(X)=p_d(X)X^d+\dots+p_1X+p_0$. Die führenden zwei Koeffizienten von p_(q,r)(X) ergeben sich zu

p_(q,r),d = q^{1 − d}p_d und $p_{(q,r),d-1}=q^{1-d}(q\,p_{d-1}-dr\,p_d)$.

Man kann also in jeder Klasse linear äquivalenter Polynome eines finden, dessen zwei führende Koeffizienten 1 und 0 sind. Dazu sind q,r so wählen, dass q^{d − 1} = p_d und $r\,dp_d=qp_{d-1}$ gelten. Da es (d-1) verschiedene Lösungen für q gibt, hat jede linear äquivalente Klasse (d-1) gleichwertige Repräsentanten. Die zu den verschiedenen Repräsentanten gehörigen Julia-Mengen entstehen durch Drehung auseinander.

Grad zwei

Untersucht man die Julia-Mengen der quadratischen Polynome, so ist jede Klasse von linear isomorphen Polynomen durch ein Polynom p(X) = X² + p₀ repräsentiert. Die Darstellung der Klassifikation der zusammenhängenden Julia-Mengen ergibt, mit p₀ = − c, die klassische Mandelbrot-Menge. Es gibt nur eine erste Einheitswurzel, somit keine Symmetrien der Mandelbrot-Menge außer der durch die komplexe Konjugation.

Grad drei

Die Klassen linear äquivalenter kubischer Polynome werden durch die Polynome p(X) = X³ + p₁X + p₀ repräsentiert. In jeder Klasse gibt es zwei solcher Repräsentanten, da es zwei zweite Einheitswurzeln q=1 und q=-1 gibt. Das zweite Polynom ist − p( − X) = X³ + p₁X − p₀. Ähnlich wie bei der klassischen Mandelbrot-Menge kann die Entscheidung, ob die Julia-Menge eines Polynoms p(X) topologisch zusammenhängend ist, auf die Zugehörigkeit der kritischen Punkte von p(X) zur Julia-Menge zurückgeführt werden. a ist kritischer Punkt von p, wenn p'(a)=3a²+p₀=0 gilt. Die Ableitung ist quadratisch, es gibt also zwei kritische Punkte. Wählt man als Parametrisierung das Paar aus einem kritischen Punkt und dem konstanten Koeffizienten, so erhält man die Polynome $p(X)=X^3-3a^2X+b\mbox{ mit }a,b\in \mathbb C$.

Die Polynome zu den Paaren (a,b), (a,-b), (-a,b) und (-a,-b) erzeugen, bis auf eine Drehung, dieselbe Julia-Menge, die Mandelbrot-Menge S zu dieser Parametrisierung hat also, neben der Symmetrie durch komplexe Konjugation, eine vierfache Symmetrie.

Schnitte durch den dreidimensionalen Körper

Schnitte durch den dreidimensionalen Körper

Die Mandelbrot-Menge S wird beschrieben durch:

$S=\left\{ (a,b)\in\mathbb C^2|\forall z_0\in\{+a,-a\};\mbox{ }\sup_{k\in\N}|p^{k}(z_0)|<\infty;\mbox{ bei }p(z)=z^3-3a^2z+b\right\}$

Visualisierung

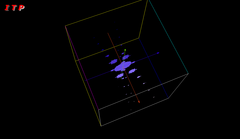
Problematisch bei der Visualisierung dieser Menge ist, dass der Parameterraum komplex zwei– und damit reell vierdimensional ist. Man hilft sich hier z. B., indem man einen der vier Parameter auswählt und ihn auf einen festen Wert setzt. Die anderen Parameter werden als Koordinaten in einem dreidimensionalen Raum verstanden. Diese Methode ist ein dreidimensionaler Schritt im vierdimensionalen Raum.

Fahrt durch den Parameterraum kubischer Polynome

Um die vierte Dimension doch noch zu erfassen, kann diese als Zeit wieder eingeführt werden. D. h. man erzeugt Einzelbilder zu einer aufsteigenden Folge des vierten Parameters und fasst diese in einer Animation zusammen. Auf diese Weise erhält man einen Film, der eine Fahrt durch ein festgelegtes Intervall auf der „vierten Achse“ darstellt.

Die Menge S hat eine fraktale Oberfläche und weist starke Parallelen mit der Mandelbrotmenge auf. Wenn man an den dreidimensionalen Objekten, die entstehen, wiederum zweidimensionale Schnitte ausführt, findet man in diesen Schnittebenen an manchen Stellen die charakteristische Form des Apfelmännchens wieder.

Weblinks

Cubic Iterations 3D (Programm zur Visualisierung des Parameterraumes)