Kubische Gleichung

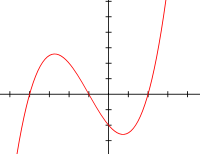Graph einer Funktion 3. Grades; die Nullstellen (y=0) sind dort, wo der Graph die x-Achse schneidet. Der Graph hat 2 Extremwerte.

Kubische Gleichungen sind algebraische Gleichungen dritten Grades, also Gleichungen der allgemeinen Form

$a \cdot x^3 + b \cdot x^2 + c \cdot x + d = 0$

mit $a,b,c,d \in \mathbb{C}$ und $a \ne 0$ in der Unbekannten $x\in\Bbb C$ (siehe auch Polynom). Im Fall a = 0 handelt es sich höchstens noch um eine quadratische Gleichung.

Die kubische Gleichung lässt sich mit Kenntnis aller drei komplexen Nullstellen x₁,x₂,x₃ auch so faktorisieren:

$a \cdot (x - x_1) \cdot (x - x_2) \cdot (x - x_3) = 0$.

Geometrisch beschreibt die reelle Variante der kubischen Gleichung eine kubische Parabel in der x-y-Ebene. Die Schnittpunkte mit der x-Achse sind die reellen Nullstellen. Da die Parabel immer von $- \infty ... + \infty \, (a > 0)$ bzw. von $+ \infty ... - \infty \, (a < 0)$ läuft und die Funktion stetig ist, muss es (nach dem Zwischenwertsatz) stets mindestens einen Schnittpunkt mit der x-Achse geben, d.h. mindestens eine reelle Nullstelle. Dies spiegelt sich auch in der algebraischen Behandlung wider.

Lösungsansätze

Raten einer Lösung

Kennt man eine Lösung x₁ exakt, so kann man das kubische Polynom mit Hilfe der Polynomdivision oder des Horner-Schemas durch (x − x₁) dividieren und erhält so eine quadratische Gleichung. Diese kann man mit Hilfe einer Lösungsformel lösen und erhält so die restlichen Lösungen der kubischen Gleichung. Dieses Verfahren ist aber nur für eine rationale Lösung x₁ praktikabel. Bereits bei der irreduziblen Gleichung x³ − 6x − 6 = 0 ist das Verfahren mit der noch relativ einfachen Lösung $x=\sqrt[3]{2} + \sqrt[3]{4}$ nicht mehr praktikabel, da die Koeffizienten der verbleibenden quadratischen Gleichung sehr kompliziert werden. In diesen Fällen lassen sich die Lösungen mit der unten genannten Cardanischen Formel leichter bestimmen.

Sind alle Koeffizienten der kubischen Gleichung ganzzahlig, so kann man versuchen, eine Lösung zu raten, das heißt, durch Probieren zu finden. Ist der führende Koeffizient a vom Betrag gleich 1, so kann man die ganzzahligen Teiler des letzten Faktors d durchprobieren (auch negative Werte!). Ist a von eins verschieden, so müssen alle Brüche, deren Zähler ein Teiler von d und deren Nenner ein Teiler von a ist, durchprobiert werden. Der Satz über rationale Nullstellen garantiert, dass man mit diesem endlichen Aufwand eine rationale Nullstelle findet, falls eine solche existiert. Sind die Koeffizienten rational, so kann man ganzzahlige Koeffizienten erreichen, indem man die Gleichung mit dem Hauptnenner aller Koeffizienten multipliziert.

Reduktion der Gleichung auf eine Normalform

Es gibt eine Reihe äquivalenter Umformungen dieser Gleichung durch Verschieben und Skalieren des Arguments und Skalieren der Gleichung, die es erlauben, bestimmten Koeffizienten feste Werte zuzuweisen und damit das nachfolgende Lösungsverfahren zu vereinfachen. Üblicherweise wird der führende Koeffizient zu 1 und der quadratische zu 0 transformiert.

Dazu wird das Argument um ein vorerst beliebiges $k\in\mathbb C$ verschoben, x = z − k, und die Gleichung durch $a \ne 0$ dividiert.

$\begin{align} 0&= (z-k)^3 + \frac b a \cdot (z-k)^2 + \frac c a \cdot (z-k) + \frac d a\\ &= z^3 + \left(- 3 k +\frac ba \right) z^2 + \left(3 k^2 - 2 \frac ba k + \frac ca\right) z + \left(- k^3 + \frac ba k^2 - \frac ca k + \frac da\right) \end{align}$.

Mit $k = \tfrac{b}{3a}$ fällt das quadratische Glied weg und es bleibt

$0= z^3 + \frac{-b^2 + 3ac}{3a^2} z +\frac{2 b^3 - 9 abc + 27 a^2d}{27a^3} = z^3 + p z + q$.

Der einfachste und historisch älteste Lösungsweg beruht nun auf dem Ansatz

$z=\sqrt[3]{A}+\sqrt[3]{B};$.

Setzt man in der Gleichung

$0=z^3+pz+q =\Big[A+B+q\Big]+\big(\sqrt[3]{A}+\sqrt[3]{B}\big)\Big[3\sqrt[3]{A}\sqrt[3]{B}+p\Big]$

die beiden Ausdrücke in eckigen Klammern separat gleich null, erhält man eine quadratische Gleichung für A und B. Führt man die entsprechende Rechnung durch, ergeben sich die Cardanischen Formeln.

Analytische Bestimmung reeller Lösungen

Es seien alle Koeffizienten der Gleichung reell. Eine weitere Vereinfachung der Gleichung nach Entfernen des quadratischen Terms ergibt sich durch Skalieren der Variablen, $z = t/s, s \ne 0$, und Multiplizieren der Gleichung mit s³,

0 = t³ + s²pt + s³q.

Ist p=0, so ist eine Lösung der Gleichung durch $z=\sqrt[3]{-q}$ gegeben.

Für $p\ne 0$ kann s so gewählt werden, dass $|s^2p|=\tfrac34$ und $d=-4\,s^3\,q>0$ gleichzeitig gilt.

Dann wird die Lösung des verbleibenden, klassisch „casus irreducibilis“ genannten Falls mit trigonometrischen und hyperbolischen, also analytischen, als Potenzreihen auswertbaren Funktionen berechnet.^[1] Es ergeben sich vier Fälle:

• $0= t^3 - 3/4 t - 1/4 d,\; 0 \le d < 1$. Es gibt drei reelle Lösungen: Sie werden durch Koeffizientenvergleich mit der trigonometrischen Gleichung cos(3x) = 4cos ³x − 3cos x = d gefunden; 3x = arccos d; t₁ = cos x; t₂ = cos(x + 120^o), t₃ = cos(x + 240^o)

• $t^3 - 3/4 t - 1/4,\; d = 1$. Es gibt zwei reelle Lösungen: Sie können aus der Kurve y = t³ − 3 / 4t = 1 / 4 direkt entnommen werden: t₁ = 1, t₂ = t₃ = − 1 / 2

• $t^3 - 3/4 t - 1/4 d,\; 1 < d$. Es gibt eine reelle Lösung: Sie wird durch Koeffizientenvergleich mit der hyperbolischen Gleichung cosh(3x) = 4cosh ³x − 3coshx = d gefunden; 3x = Arcosh d; t = cosh x

• $t^3 + 3/4 t - 1/4 d,\ 0 \le d$. Es gibt eine reelle Lösung: Auch hier wird die Lösung durch Koeffizientenvergleich mit einer hyperbolischen Gleichung gefunden: sinh(3x) = 4sinh ³x + 3sinh x = d; 3x = Arsinh d; t = sinhx

Siehe auch

• Lineare Gleichung
• Quartische Gleichung
• Omar Khayyām
• Gerolamo Cardano

Weblinks

• Online-Tool zum Berechnen von Polynomen n-ter Ordnung
• Kubische Gleichung - JavaScript
• Leitfaden zur Lösung kubischer Gleichungen

Einzelnachweise

 Commons: Cubic polynomials – Sammlung von Bildern, Videos und Audiodateien

1. ↑ Peter Gabriel: Matrizen, Geometrie, Lineare Algebra. Birkhäuser 1996, ISBN 3-7643-5376-7