- Lineare Funktion
-
Der Begriff lineare Funktion wird nicht einheitlich gebraucht. Einerseits bezeichnet dieser Begriff eine Funktion, die die Eigenschaft der Linearität erfüllt, also eine lineare Abbildung ist. Lineare Funktionen in diesem Sinne findet man z. B. in der Differentialgeometrie, wobei es sich um lineare Abbildungen von einem (Tangential-)Vektorraum in die reellen Zahlen handelt.
Andererseits wird mit dem Begriff lineare Funktion oft (besonders in der Schule) eine Abbildung der Form
 ,
,
also ein Polynom ersten Grades, bezeichnet. Eine solche Funktion wird auch allgemeine lineare Funktion oder linear-inhomogene Funktion genannt (siehe dazu auch Geradengleichung). Im mathematisch strengen Sinn handelt es sich dabei jedoch um eine affine Abbildung. Für den Spezialfall n = 0 wird daraus eine lineare Funktion im eigentlichen Sinne, auch als homogene lineare Funktion oder Proportionalität bezeichnet.
Lineare Funktionen sind die einfachsten Funktionen in der Mathematik. Sie sind stetig und differenzierbar. Viele Probleme lassen sich für lineare Funktionen leicht lösen; daher versucht man oft, komplizierte Problemstellungen durch lineare Zusammenhänge zu approximieren.
Inhaltsverzeichnis
Graph
Der Graph einer linearen Funktion ist immer eine Gerade. In kartesischen Koordinaten (x,y) erfüllen solche Geraden also die Gleichung
 ,
,
wobei x (die Abszisse) unabhängige und y (die Ordinate) abhängige Variablen sind.
(Manchmal werden auch andere Benennungskonventionen verwendet, z. B. f(x) = ax + b, f(x) = mx + c, f(x) = mx + b, f(x) = mx + t oder y = ax + b. In Österreich wird häufig y = kx + d verwendet, in der Schweiz hingegen y = mx + q.)Diese Form bezeichnet man auch als die Normalform einer linearen Funktion. Ihre Komponenten lassen sich wie folgt interpretieren:
- Die Zahl m gibt den linearen Faktor oder die Steigung der Geraden an.
- Die Zahl n ist die Inhomogenität, der Ordinatenabschnitt, die Verschiebungskonstante oder der y-Achsenabschnitt.
Der Graph einer linearen Funktion kann niemals parallel zur y-Achse verlaufen, da sonst einem x-Wert mehrere y-Werte zugeordnet wären. Dies würde der Definition einer Funktion als eindeutige Zuordnung widersprechen.
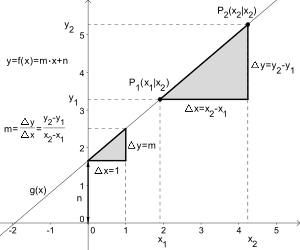
Bestimmung des Funktionsterms aus zwei Punkten
Es wird vorausgesetzt, dass die Punkte (x1 | y1) und (x2 | y2) auf dem Graphen der linearen Funktion f liegen und voneinander verschieden sind.
Die Steigung m lässt sich errechnen aus
 .
.
Der y-Achsenabschnitt b ergibt sich aus
 . bzw. :
. bzw. : .
.
Der gesuchte Funktionsterm f(x) ist also gegeben durch
oder einfacher durch
 .
.
Zusammenfassung
Funktionsgleichung
- Eine Funktion
 mit
mit  heißt ganzrationale Funktion 1. Grades oder lineare Funktion.
heißt ganzrationale Funktion 1. Grades oder lineare Funktion. - Der Funktionsgraph stellt eine Gerade dar.
Achsenschnittpunkte
- Schnittpunkt mit der y-Achse:

- Schnittpunkt mit der x-Achse:

Steigung

- Die Steigung des Graphen einer linearen Funktion mit der Funktionsgleichung
 mit
mit  lässt sich am Koeffizienten
lässt sich am Koeffizienten  ablesen.
ablesen. - Berechnet wird er mit:
 In Kurzform:
In Kurzform: 
Funktionsgleichung aufstellen
- Die Steigung a1 = a und ein Punkt P1(x1 | y1), der auf der Geraden liegt, seien bekannt.
- Ansatz: f(x) = ax + a0

- Die Koordinaten zweier Punkte P1(x1 | y1) und P2(x2 | y2), die auf der Geraden liegen, seien bekannt.
- Zuerst wird der Steigungsfaktor berechnet:


- oder

Schnittpunkt zweier Geraden
- Ansatz:
 x - Wert vom Schnittpunkt der beiden Geraden.
x - Wert vom Schnittpunkt der beiden Geraden.  als Schnittpunkt der beiden Geraden.
als Schnittpunkt der beiden Geraden.
Orthogonale Geraden
- Für die Steigung zweier senkrecht aufeinanderstehender Geraden g1 und g2 gilt:
 bzw.
bzw.  bzw.
bzw. 
Beispiel
Zwei verschiedene Telefongesellschaften A und B bieten für das gleiche Handy verschiedene Tarife an. Gesellschaft A bietet den folgenden Vertrag: 20 € monatliche Grundgebühr und jede angefangene Minute 0,07 € an Telefonie. Gesellschaft B jedoch: 10 € Grundgebühr und dafür aber 0,10 € pro angefangener Minute.
Die Angebote der Gesellschaften werden in zwei mathematische Gleichungen ausgedrückt: für A: y = 0,07x + 20 und für B: y = 0,10x + 10
x sind die jeweiligen abtelefonierten Minuten und y ist der zu zahlende Rechnungsbetrag am Ende eines Monats. Anhand der Gleichungen würden erfahrene Menschen sofort sehen, welche ab wann günstiger ist. Doch am klügsten wäre es jetzt, die Gleichungen gleichzusetzen.
Wir nennen die Gleichung von A f(x) und die Gleichung von B g(x). Daraus folgt, dass f(x) = g(x) ist und so können wir die Gleichungen gleichsetzen und erhalten das Folgende:

Anhand dieses Ergebnisses können wir y ausrechnen und nehmen dazu eine beliebige Gleichung, hier g(x):

In dem wir nun x und y ausgerechnet haben, wissen wir, wo sich diese zwei Geraden schneiden, nämlich im Schnittpunkt S (333,33|43,33). Dies ist aber nur hilfreich, wenn wir diese Geraden zeichnen könnten. Für den nicht-zeichnerischen Gebrauch sehen wir uns einfach die x- und y-Werte an:
Wir wissen nun, dass uns bei beiden Anbietern 333,33 Minuten den gleichen Betrag von 43,33 € kosten würden. Die eigentliche Frage, die sich uns stellt, ist: Wie sieht es mit Minutenzahlen unter und über 333,33 aus?
1. Fall: Bei unter 333,33 Minuten - wo ist es günstiger und wo teurer? Bei Anbieter A für 300 Minuten:
 und ausgerechnet: y = 41 [€]
und ausgerechnet: y = 41 [€]und bei Anbieter B für 300 Minuten:
 und ausgerechnet: y = 40 [€]
und ausgerechnet: y = 40 [€]Daraus ergibt sich: Bei einer Minutenanzahl unter 333,33 Minuten, die bei beiden gleich kostet, lohnt es sich mehr beim Anbieter B.
2. Fall: Bei über 333,33 Minuten - wo ist es günstiger und wo teurer? Bei Anbieter A für 340 Minuten:
 und somit ist y = 43,80 [€]
und somit ist y = 43,80 [€]und bei Anbieter B für 340 Minuten:
 und somit ist y = 44 [€]
und somit ist y = 44 [€]Daraus ergibt sich: Bei einer Minutenanzahl von über 333,33 Minuten, die bei beiden gleich kostet, lohnt es sich mehr beim Anbieter A.
Dies ist nur ein winziges Beispiel aus dem Alltag, in dem lineare Funktionen hilfreich sein können.
Den Zusammenhang zwischen Umfang u und Radius r eines Kreises beschreibt die lineare Funktion
Da der Achsenabschnitt null ist, handelt es sich hierbei sogar um eine Proportionalität. Für das Steigungsdreieck gilt dann entsprechend:
 oder
oder 
Eine oft gestellte Denksportaufgabe setzt nun voraus, dass man ein Seil um den Äquator gespannt hat, also ca. 40.000 km lang, und dieses dann um nur einen Meter verlängert und das Seil gleichmäßig überall entsprechend von der Erdoberfläche abhebt. Die Frage lautet dann, ob man anschließend einen Tennisball unter dem Seil durchschieben kann. Das Gefühl sagt einem, dass der Effekt so klein sein sollte, dass das Seil sich kaum merkbar vom Boden heben sollte.
Die obige Funktion sagt aber, dass das Steigungsdreieck überall entlang der Geraden gleich ist, also überall eine Verlängerung der Umfangslinie um Δu eine Vergrößerung des Radius um Δr bewirken muss. Wenn Δu=1 m ist, ergibt sich demnach Δr zu etwa 15 cm. Der Tennisball passt also tatsächlich unter dem Seil hindurch.
Ableitung und Stammfunktion
Die Ableitung von
 ist
ist  , also immer eine konstante Funktion (Eine lineare Funktion lässt sich auch als Funktion mit konstanter Ableitung definieren), da die Ableitung die Steigung der Tangente im Punkt
, also immer eine konstante Funktion (Eine lineare Funktion lässt sich auch als Funktion mit konstanter Ableitung definieren), da die Ableitung die Steigung der Tangente im Punkt  angibt.
angibt.Eine Stammfunktion von
 ist
ist  . Dies lässt sich folgendermaßen zeigen:
. Dies lässt sich folgendermaßen zeigen:Literatur
- Manfred Leppig: Lernstufen Mathematik. Girardet 1981, ISBN 3-7736-2005-5, S. 61-74
Weblinks
Wikimedia Foundation.