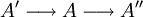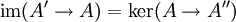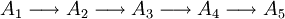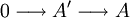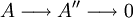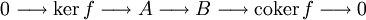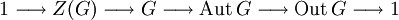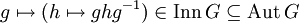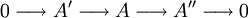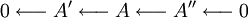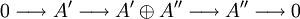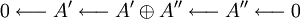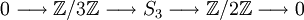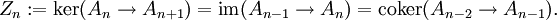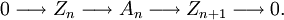Kurze exakte Sequenz

Der Begriff der exakten Sequenz spielt eine zentrale Rolle im mathematischen Teilgebiet der homologischen Algebra. Besonders wichtig sind die kurzen exakten Sequenzen.

Definition

Eine Sequenz

$A'\longrightarrow A\longrightarrow A''$

von Objekten und Morphismen in einer geeigneten Kategorie heißt exakt an der Stelle A, wenn

$\mathrm{im}(A'\to A)=\ker(A\to A'')$

gilt, d.h. wenn das Bild eines Pfeils gleich dem Kern des nächsten ist. Eine längere Sequenz

$A_1\longrightarrow A_2\longrightarrow A_3\longrightarrow A_4\longrightarrow A_5$

heißt exakt, wenn sie exakt an den Stellen A₂, A₃ und A₄ ist (analog für kürzere oder längere Sequenzen).

Geeignet in diesem Sinne ist eine Kategorie offenbar nur dann, wenn sinnvoll von Kern und Bild gesprochen werden kann. Dies ist der Fall für alle abelschen Kategorien, aber auch beispielsweise für die Kategorie Grp der Gruppen und Gruppenhomomorphismen. In der Tat ist Grp üblicherweise die einzige nicht-abelsche Kategorie, in der exakte Sequenzen betrachtet werden.

Beispiele

• Eine Sequenz

$0\longrightarrow A'\longrightarrow A$

ist genau dann exakt, wenn 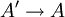$A'\to A$ ein Monomorphismus ist.

• Eine Sequenz

$A\longrightarrow A''\longrightarrow0$

ist genau dann exakt, wenn 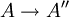$A\to A''$ ein Epimorphismus ist.

• Für jeden Homomorphismus 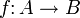$f\colon A\to B$ von Vektorräumen (abelschen Gruppen, Moduln, jeden Morphismus einer abelschen Kategorie) ist die Sequenz

$0\longrightarrow\ker f\longrightarrow A\longrightarrow B\longrightarrow\mathrm{coker}\,f\longrightarrow0$

exakt. In Grp ist die Sequenz jedoch bei B nur exakt, wenn das Bild von f ein Normalteiler in B ist. Auch in additiven, aber nicht abelschen Kategorien ist die Exaktheit nicht notwendigerweise gegeben.

• Für eine Gruppe G seien
  • Z(G) das Zentrum,
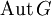  • $\mathrm{Aut}\,G$ die Gruppe der Automorphismen,
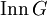  • $\mathrm{Inn}\,G$ die Gruppe der inneren Automorphismen und
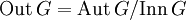  • $\mathrm{Out}\,G=\mathrm{Aut}\,G/\mathrm{Inn}\,G$ die Gruppe der äußeren Automorphismen

von G. Dann ist die Sequenz

$1\longrightarrow Z(G)\longrightarrow G\longrightarrow\mathrm{Aut}\,G\longrightarrow\mathrm{Out}\,G\longrightarrow1$

exakt. Der mittlere Pfeil ist dabei durch

$g\mapsto(h\mapsto ghg^{-1})\in\mathrm{Inn}\,G\subseteq\mathrm{Aut}\,G$

gegeben.

Kurze exakte Sequenzen

Eine exakte Sequenz der Form

$0\longrightarrow A'\longrightarrow A\longrightarrow A''\longrightarrow0$

heißt kurze exakte Sequenz.

Zerfallende kurze exakte Sequenzen

Eine kurze exakte Sequenz zerfällt, wenn 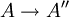$A\to A''$ einen Schnitt hat. Vereinzelt wird anstatt zerfällt, auch die Bezeichnung spaltet auf benutzt, die auf eine nicht ganz korrekte Übersetzung des englischen Begriff split zurückzuführen ist.

In einer additiven Kategorie folgt hieraus auch, dass 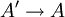$A'\to A$ eine Retraktion hat, dass die entstehende Sequenz

$0\longleftarrow A'\longleftarrow A\longleftarrow A''\longleftarrow 0$

ebenfalls exakt ist und dass diese Sequenzen isomorph zu

$0\longrightarrow A'\longrightarrow A'\oplus A''\longrightarrow A''\longrightarrow0$

bzw.

$0\longleftarrow A'\longleftarrow A'\oplus A''\longleftarrow A''\longleftarrow 0$

sind.

Zerfällt eine kurze exakte Sequenz in der Kategorie der Gruppen, ergibt sich daraus lediglich eine Operation von A'' auf A', und dass A semidirektes Produkt von A' und A'' bezüglich dieser Operation ist. Beispielsweise ist die zyklische Gruppe 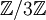$\mathbb{Z}/3\mathbb{Z}$ Untergruppe der symmetrischen Gruppe S₃, woraus sich die kurze exakte Sequenz

$0\longrightarrow \mathbb{Z}/3\mathbb{Z}\longrightarrow S_3 \longrightarrow \mathbb{Z}/2\mathbb{Z}\longrightarrow0$

ergibt; indem man das nicht-neutrale Element der 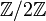$\mathbb{Z}/2\mathbb{Z}$ auf ein Element der Ordnung 2 in S₃ abbildet, erhält man eine Spaltung.

Aufteilung einer langen exakten Sequenz

Jede lange exakte Folge lässt sich in kurze exakte Folgen zerlegen, indem man Kerne und Kokerne einfügt: Ist

$A_1\longrightarrow A_2\longrightarrow A_3\longrightarrow A_4\longrightarrow A_5$

eine exakte Sequenz, so sei

$Z_n:=\ker(A_n\to A_{n+1})=\mathrm{im}(A_{n-1}\to A_n)=\mathrm{coker}(A_{n-2}\to A_{n-1}).$

Dann gibt es kurze exakte Sequenzen

$0\longrightarrow Z_n\longrightarrow A_n\longrightarrow Z_{n+1}\longrightarrow0.$

Ist (A _* ) ein Kettenkomplex, so ist die Exaktheit all dieser kurzen Sequenz äquivalent zur Exaktheit der langen Sequenz.

Erweiterungen

Im Kontext einer kurzen exakten Sequenz

$0\longrightarrow A'\longrightarrow A\longrightarrow A''\longrightarrow0$

sagt man auch, dass A eine Erweiterung von A'' durch A' ist.

Siehe Ext (Mathematik), Gruppenkohomologie

Siehe auch

• Exakter Funktor
• Kettenkomplex