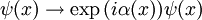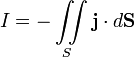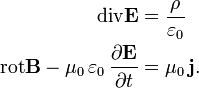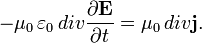- Ladungserhaltungssatz
-
In der Elektrizitätslehre bzw. Elektrodynamik gelten Erhaltungssätze für die elektrische Ladung: die Summe der elektrischen Ladung bleibt im abgeschlossenen System immer konstant. Wenn geladene Teilchen erzeugt oder vernichtet werden, dann geschieht dies immer in gleichen Quantitäten beider Vorzeichen.
Im Sinn des Noetherschen Theorems sind die Erhaltungssätze für die Ladung mit einer Symmetrieeigenschaft der Theorie, ihrer Invarianz unter Eichtransformationen, verbunden. Im Falle der (Quanten-)-Elektrodynamik ist das die Invarianz unter lokalen Eichtransformationen (Eichgruppe U(1), Multiplikation mit einem komplexen Phasenfaktor) der Wellenfunktion geladener Teilchen:
Entsprechende Ladungserhaltungssätze gibt es auch für andere Eichtheorien, wie die Quantenchromodynamik (Erhaltung der Farbladung, zugehörige Eichgruppe SU (3)) und die Eichtheorie der elektro-schwachen Wechselwirkung (Eichgruppe SU(2) x U(1)), die im Standardmodell der Elementarteilchenphysik die Quantenelektrodynamik verallgemeinert.
Herleitung der Differentialgleichung für die Erhaltung der elektrischen Ladung
Wie bei der Massenerhaltung (Kontinuitätsgleichung) kann man auch die Ladungserhaltung als Differentialgleichung formulieren. Sie wird im folgenden hergeleitet.
Der Strom, der aus einem Volumen V fließt, ist
wobei über den Rand S des Volumens integriert wird und das Produkt als inneres Produkt des Stromdichtevektors mit dem Normalenvektor der Fläche zu verstehen ist.
Mit dem Integralsatz von Gauß folgt daraus:
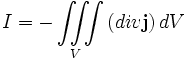 .
.
Und da der Stromfluß aus dem Volumen gleich der zeitlichen Änderung der Ladung im Volumen ist, gilt:
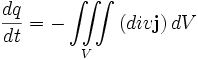 .
.
Ladung und Ladungsdichte sind über
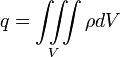 .
.
verbunden, so daß man erhält:
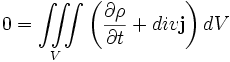 .
.
Da das für jedes zusammenhängende Volumen gilt, erhält man schließlich:
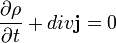 .
.
Sie ist von der gleichen mathematischen Form wie die aus der Massenerhaltung folgende Kontinuitätsgleichung (man hat nur Ladungsdichte durch Massendichte usw. zu ersetzen).
Die Erhaltung der elektrischen Ladung steckt auch implizit in den Maxwellgleichungen:
Weil die Divergenz einer Rotation verschwindet folgt bei Bildung der Divergenz der zweiten Gleichung
Setzt man in diese Beziehung die zeitliche Ableitung der ersten Gleichung ein, so folgt
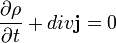 .
.
Wikimedia Foundation.