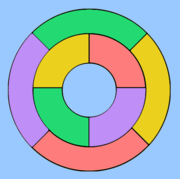
Landkartenfärbungsproblem

Der Vier-Farben-Satz (früher auch als Vier-Farben-Vermutung oder Vier-Farben-Problem bekannt) ist ein mathematischer Satz und besagt, dass vier Farben immer ausreichen, um eine beliebige Landkarte in der euklidischen Ebene so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen. Der Satz findet Anwendung in der Graphentheorie, Topologie und Kartografie.

Dies gilt unter den Einschränkungen, dass ein gemeinsamer Punkt nicht als „Grenze“ zählt und jedes Land aus einer zusammenhängenden Fläche besteht, also keine Exklaven vorhanden sind.

Beispiel einer Vier-Färbung

Geschichte

Der Satz wurde erstmals 1852 von Francis Guthrie als Vermutung aufgestellt, als er die Grafschaften von England färben wollte. Es war offensichtlich, dass drei Farben nicht ausreichten und man fünf in keinem konstruierten Beispiel brauchte. In einem Brief des Londoner Mathematikprofessors Augustus De Morgan vom 23. Oktober 1852 an den irischen Kollegen William Rowan Hamilton wurde die Vermutung erstmals diskutiert und veröffentlicht: „Genügen vier oder weniger Farben, um die Länder einer Karte so zu färben, dass benachbarte Länder verschiedene Farben tragen?“.

Der englische Mathematiker Arthur Cayley stellte das Problem 1878 der mathematischen Gesellschaft Londons vor. Innerhalb nur eines Jahres fand Alfred Kempe einen scheinbaren Beweis für den Satz. Elf Jahre später, 1890, zeigte Percy Heawood, dass Kempes Beweisversuch fehlerhaft war. Ein zweiter fehlerhafter Beweisversuch, 1880 von Peter Guthrie Tait veröffentlicht, konnte ebenfalls elf Jahre lang nicht widerlegt werden. Erst 1891 zeigte Julius Petersen, dass auch Taits Ansatz nicht korrekt war. Heawood gab im Jahre 1890 mit der Widerlegung von Kempes „Vier-Farben-Beweis“ zusätzlich einen Beweis für den Fünf-Farben-Satz an, womit eine obere Grenze für die Färbung von planaren Graphen zum ersten Mal fehlerfrei bewiesen wurde. In Kempes fehlerhaftem Versuch steckten bereits grundlegende Ideen, die zum späteren Beweis durch Appel und Haken führten.

Heinrich Heesch entwickelte in den 1960er und 1970er Jahren Verfahren, um einen Beweis mit Hilfe des Computers zu suchen.

Darauf aufbauend konnten Kenneth Appel und Wolfgang Haken 1977 einen solchen finden. Der Beweis reduzierte die Anzahl der problematischen Fälle von Unendlich auf 1.936 (eine spätere Version sogar 1.476), die durch einen Computer einzeln geprüft wurden.

1980 hinterlegte der britische Mathematiker George Spencer-Brown in der Royal Society ein Manuskript seines Beweises zum Vier-Farben-Satz. Der Beweis ist als Anhang in die deutsche Ausgabe seines Buches Laws of Form aufgenommen worden.^[1]

1996 konnten Neil Robertson, Daniel Sanders, Paul Seymour und Robin Thomas einen modifizierten Beweis finden, der die Fälle auf 633 reduzierte. Auch diese mussten per Computer geprüft werden.

2004 haben Benjamin Werner und Georges Gonthier einen formalen Beweis des Satzes in dem Beweisassistenten Coq konstruiert. Dadurch ist es nicht mehr nötig, den Computerprogrammen zur Überprüfung der Einzelfälle zu vertrauen, sondern „nur“ dem Coq-System.

Der Vier-Farben-Satz war das erste große mathematische Problem, das mit Hilfe von Computern gelöst wurde. Deshalb wurde der Beweis von einigen Mathematikern nicht anerkannt, da er nicht direkt durch einen Menschen nachvollzogen werden kann. Schließlich muss man sich auf die Korrektheit des Compilers und der Hardware verlassen. Auch die mathematische Eleganz des Beweises wurde kritisiert („Ein guter Beweis liest sich wie ein Gedicht – dieser sieht aus wie ein Telefonbuch!“).

Fehlerhafte Gegenbeweise

Diese Karte wurde mit fünf Farben eingefärbt…

… und es ist notwendig, mindestens vier der zehn Regionen umzufärben, um eine Färbung mit nur vier Farben zu erreichen.

Wie viele offene Probleme der Mathematik hat der Vier-Farben-Satz eine Menge fehlerhafter Beweise und Gegenbeweise provoziert. Manche haben der öffentlichen Prüfung über Jahrzehnte standgehalten, bis sie als falsch erkannt wurden. Viele andere, hauptsächlich von Amateuren entwickelte, sind niemals veröffentlicht worden.

Häufig enthalten die einfachsten „Gegenbeispiele“ eine Region, welche alle anderen Regionen berührt. Dies erzwingt, um mit vier Farben auszukommen, die restlichen Regionen mit nur drei Farben auszufüllen. Da der Vier-Farben-Satz gilt, ist dies immer möglich. Die Person, die die Karte entwickelt, konzentriert sich aber häufig auf diese große Region und übersieht dabei schnell, dass es tatsächlich möglich ist.

Dieser Trick kann verallgemeinert werden; es ist leicht Karten zu konstruieren, auf denen es unmöglich ist, mit vier Farben auszukommen, wenn die Farben einiger Regionen im Voraus festgelegt wurden. Ein oberflächlicher Überprüfer des Gegenbeispiels wird oft nicht daran denken, diese Regionen umzufärben, so dass das Gegenbeispiel gültig wirkt.

Andere falsche Gegenbeweise verletzen die Annahmen des Satzes in unerwarteter Weise, wie zum Beispiel durch Verwendung von Regionen, die aus mehreren, getrennten Bereichen bestehen, oder durch Verbieten von gleichfarbigen Regionen, die sich nur an einem Punkt berühren.

Formalisierung

Darstellung der Formulierung in der Graphentheorie

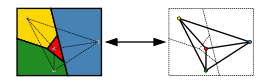
Formal lässt sich das Problem am einfachsten mit Hilfe der Graphentheorie beschreiben. Man fragt, ob die Knoten jedes planaren Graphen mit maximal vier Farben so gefärbt werden können, dass keine benachbarten Knoten die gleiche Farbe tragen. Oder kürzer: „Ist jeder planare Graph 4-färbbar?“ Dabei wird jedem Land der Karte genau ein Knoten zugewiesen; die Knoten angrenzender Länder werden miteinander verbunden.

Das Vier-Farben-Problem ist ein Spezialfall der Heawood-Vermutung. Das klassische Vier-Farben-Problem betrifft Landkarten, die auf einer Ebene oder Kugeloberfläche liegen. Die Heawood-Vermutung stellt das analoge Problem für allgemeine Oberflächen, etwa die Kleinsche Flasche (6 Farben), das Möbiusband (6 Farben), die Projektive Ebene (6 Farben) und den Torus (7 Farben). Interessanterweise ist die Verallgemeinerung – abgesehen vom Spezialfall für Ebenen oder Kugeloberflächen – wesentlich leichter zu beweisen als der Vier-Farben-Satz und kommt ohne Computerhilfe aus. J. W. Ted Youngs und Gerhard Ringel konnten im Jahre 1968 erstmal die Heawood-Vermutung für alle anderen Fälle beweisen (Satz von Ringel-Youngs). Der Vier-Farben-Satz wird also nicht durch diesen Beweis verifiziert, sondern muss gesondert behandelt werden.

Bemerkung

Wenn (so wie in der Realität häufig der Fall) ein Land auf mehrere nicht-angrenzende Gebiete verteilt ist (Kolonien, Enklaven, Exklaven, …), dann ist der zugehörige Graph nicht notwendigerweise planar und es sind möglicherweise mehr als vier Farben zur Färbung notwendig.

Fußnoten

1. ↑ G. Spencer-Brown: Gesetze der Form. Lübeck 1997, S. 143–188

Literatur

• Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas: A new proof of the four-colour theorem. In: Electronic Research Announcements of the American Mathematical Society. 2/1996. S. 17–25
• Kenneth Appel, Wolfgang Haken: Every Planar Map is Four Colorable. In: Contemp. Math. vol. 98, Amer. Math. Soc., Providence, RI, 1989
• George Spencer-Brown: Laws of Form. Appendix 5. Two proofs of the four-colour map theorem.
• Georges Gonthier: A computer-checked proof of the Four Colour Theorem. unveröffentlicht
• Rudolf Fritsch, Gerda Fritsch: Der Vierfarbensatz: Geschichte, topologische Grundlagen und Beweisidee. BI-Wissenschaftverlag, 2004, ISBN 3-411-15141-2

Weblinks

• Zusammenfassung des Beweises von Robertson, Sanders, Seymour, Thomas auf der Homepage von Robin Thomas (englisch)